In the last session you used code that to solve the advertising campaign problem. As a reminder:

There are number of cities which we would like to broadcast an advertisement to.
Each city has their own radio station to transmit the advertisement.
If a city is chosen to broadcast the advertisement, then all cities close by can also hear the advertisement (‘close by’ is determined by a network, or adjacency matrix).
What is cities should we broadcast from in order for the advertisement to reach every city, that would minimise the number of broadcasts?

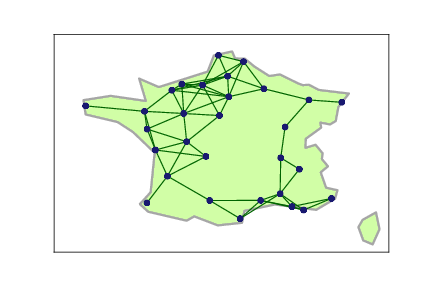
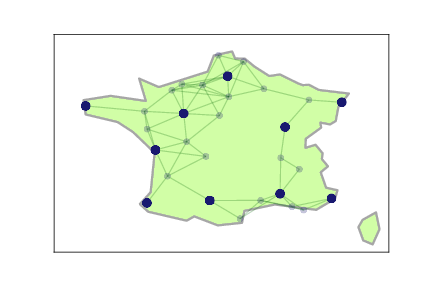
Thinking of this in terms of graphs, this is an example of finding a dominating set. You may find throughout your degree and beyond, that well defined and commonly studied problems have clever and specific methods of solving them. Recognising that your problem can be generalised to one of these well studied problems, and then identifying the appropriate solution method, is a skill you will learn with experience. Otherwise, a more generic solution method is required.

Generic solution methods

Specialised solution methods are not always known. Naive or generic methods can be used instead; or there are cleverer methods that allow us to intelligently and efficiently navigate through the set of potential solutions, these are called heuristics (you may study these further in your degree). In order to do this, we need to be able to easily check how well a solution performs, even if finding the optimal solution is difficult. Naive heuristics usually follow the following outline:

Evaluate initial guess at solution
Change the solution slightly
Evaluate solution
If better than previous best, call this previous best
Go back to 2.

In today’s task you will be thinking about how you can write an algorithm to solve the advertising campaign problem in this way. What does ‘evaluate’ mean in this case? What does a ‘solution’ look like? How would you ‘change’ the solution? Are there any other steps you could add that to make the algorithm better or more efficient?

The heart of the problem is the adjacency matrix, let’s recap.

Adjacency matrices

You used adjacency matrices in the previous section. Here is a reminder:

The adjacency matrix of a simple graph is a matrix with rows and columns labelled by graph vertices, with a 1 or 0 in position \((v_i, v_j)\) according to whether \(v_i\) and \(v_j\) are adjacent or not.

An example:

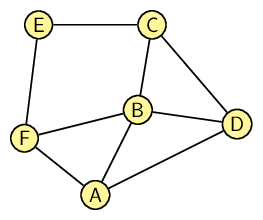
\[\begin{array}{c c} & \begin{array}{c c c c c c} A & B & C & D & E & F \\ \end{array} \\ \begin{array}{c c c c c c} A \\ B \\ C \\ D \\ E \\ F \end{array} & \left( \begin{array}{c c c c c c} 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 & 1 & 1 \\ \end{array} \right) \end{array}\]

Think about how this is connected to the advertising campaign problem. If an advert is broadcast in city A, then all cities with a 1 in the A row will be able to hear it. (Usually an adjacency matrix has 0s in the diagonal, but it has been adapted in this case for a more meaningful interpretation.)

Task

In groups of 4 or 5, write down in English a precise algorithm for solving the advertising campaign problem. It should take as inputs the adjacency matrix, and any other parameters you feel is needed. It should output a list of cities.

You should consider:

Mathematically, what does a ‘solution’ look like?
How would we generate or change solutions?
What is the easiest way to check if a solution is feasible (it is a dominating set, it does cover every city)?
How can we compare two feasible solutions?
When should the algorithm stop?

Some advanced questions to consider:

What information do you need to store?
What does the rank of the adjacency matrix give you? How could this help?
Are you confident your solution is the optimal?

Previous - Home - Next