Question A

Consider the sets \(A = \{x, 7, 13\}\) and \(B = \{x, 2, 14, 15\}\).

Write down \(A \cup B\).

SOLUTION: \(A \cup B = \{x, 2, 7, 13, 14, 15\}\)
Write down \(A \cap B\).

SOLUTION: \(A \cap B = \{x\}\)
Write down the power sets of \(A\) and \(B\). SOLUTION:

The power set of A is \(P(A) = \{\{x\}, \{7\}, \{13\}, \{x, 7\}, \{x, 13\}, \{7, 13\}, \{x, 7, 13\}\}\), and the power set of B is \(P(B) = \{\{x\}, \{2\}, \{14\}, \{15\}, \{x, 2\}, \{x, 14\}, \{x, 15\}, \{2, 14\},\{2, 15\}, \{14, 15\}, \{x, 2, 14\}, \{x, 2, 15\}, \{x, 14, 15\}, \{2, 14, 15\}, \{x, 2, 14, 15\}\}\).
Write down \(\lvert A \setminus B \rvert\)

SOLUTION: \(A \setminus B = \{7, 13\}\), therefore \(\lvert A \ B \rvert = 2\).
Let \(C\) be the set of values that are impossible for \(x\) to take. Write down \(C\).

SOLUTION: \(C = \{2, 7, 13, 14, 15\}\) as sets must contain unique elements.

Question B

Consider the empty Venn diagram below:

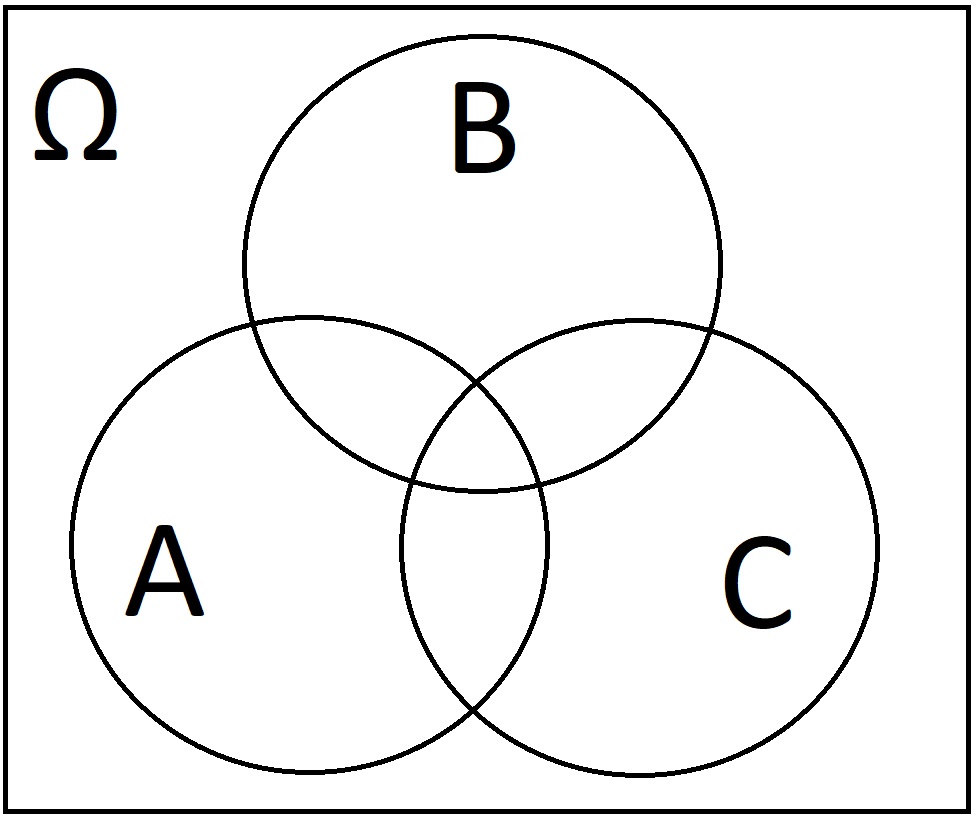
Shade in \(A \cup B\)

SOLUTION:
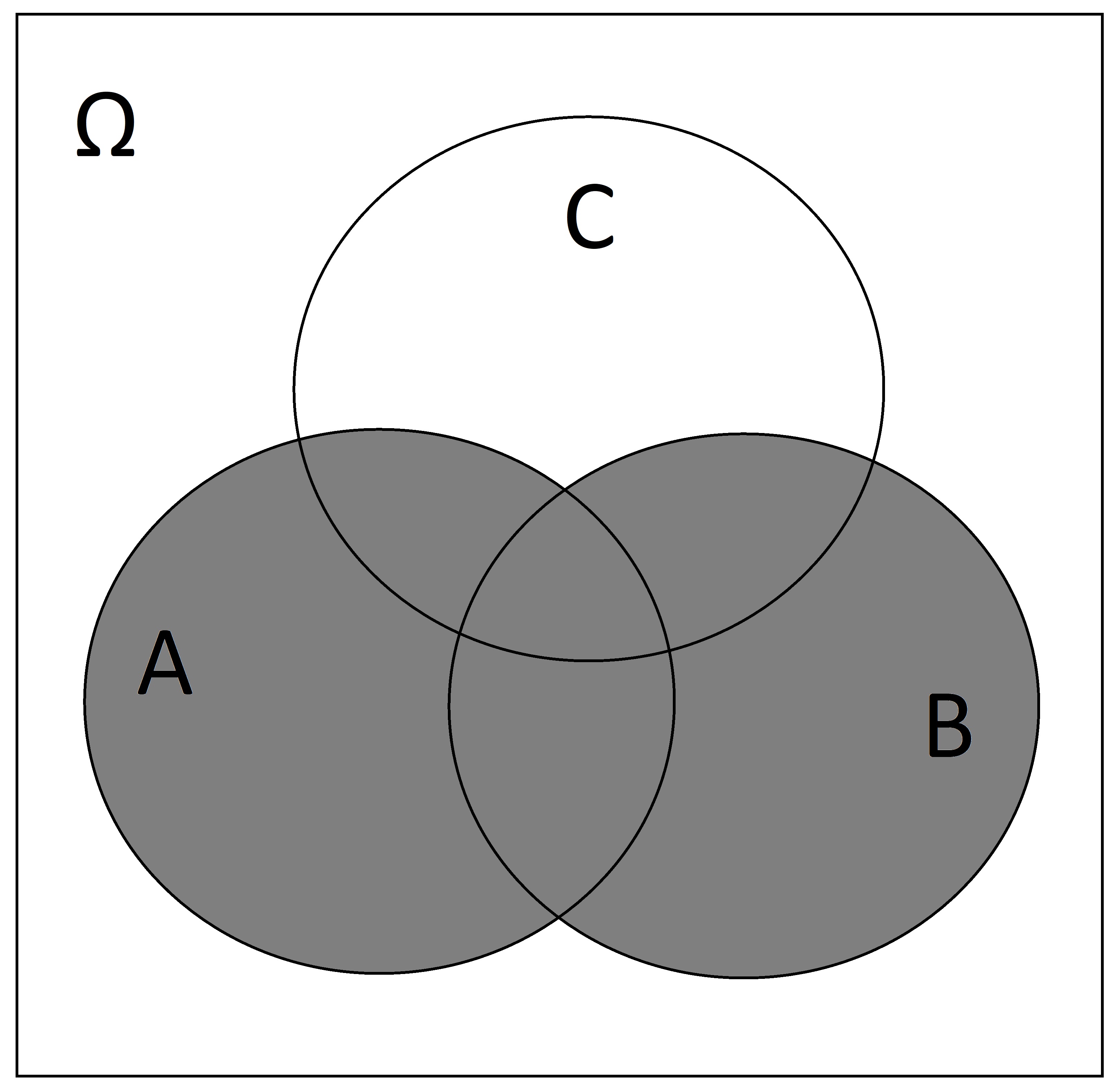
Shade in \(A \cap C\)

SOLUTION:
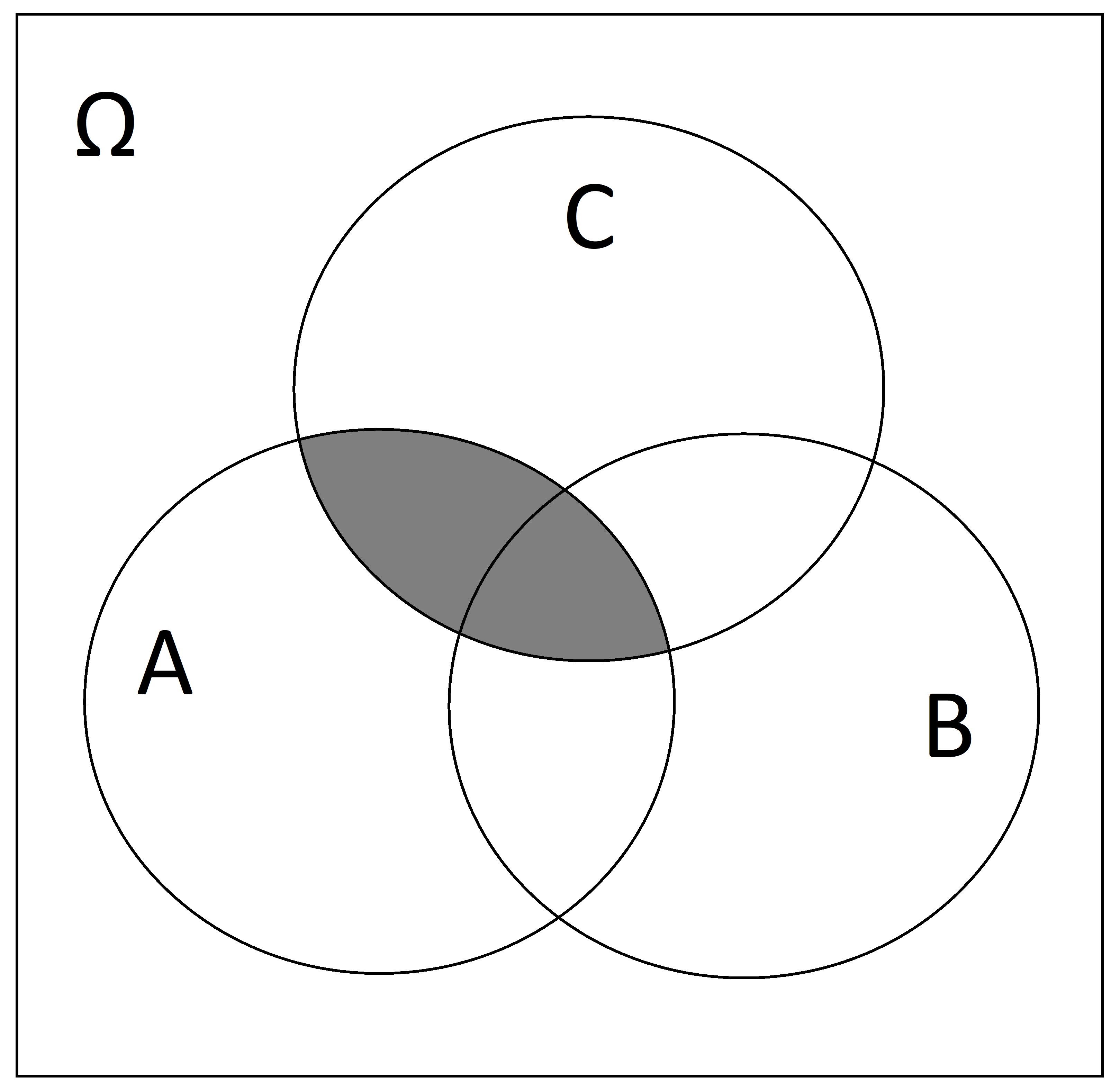
Shade in \(\overline{A \cup B \cup C}\)

SOLUTION:
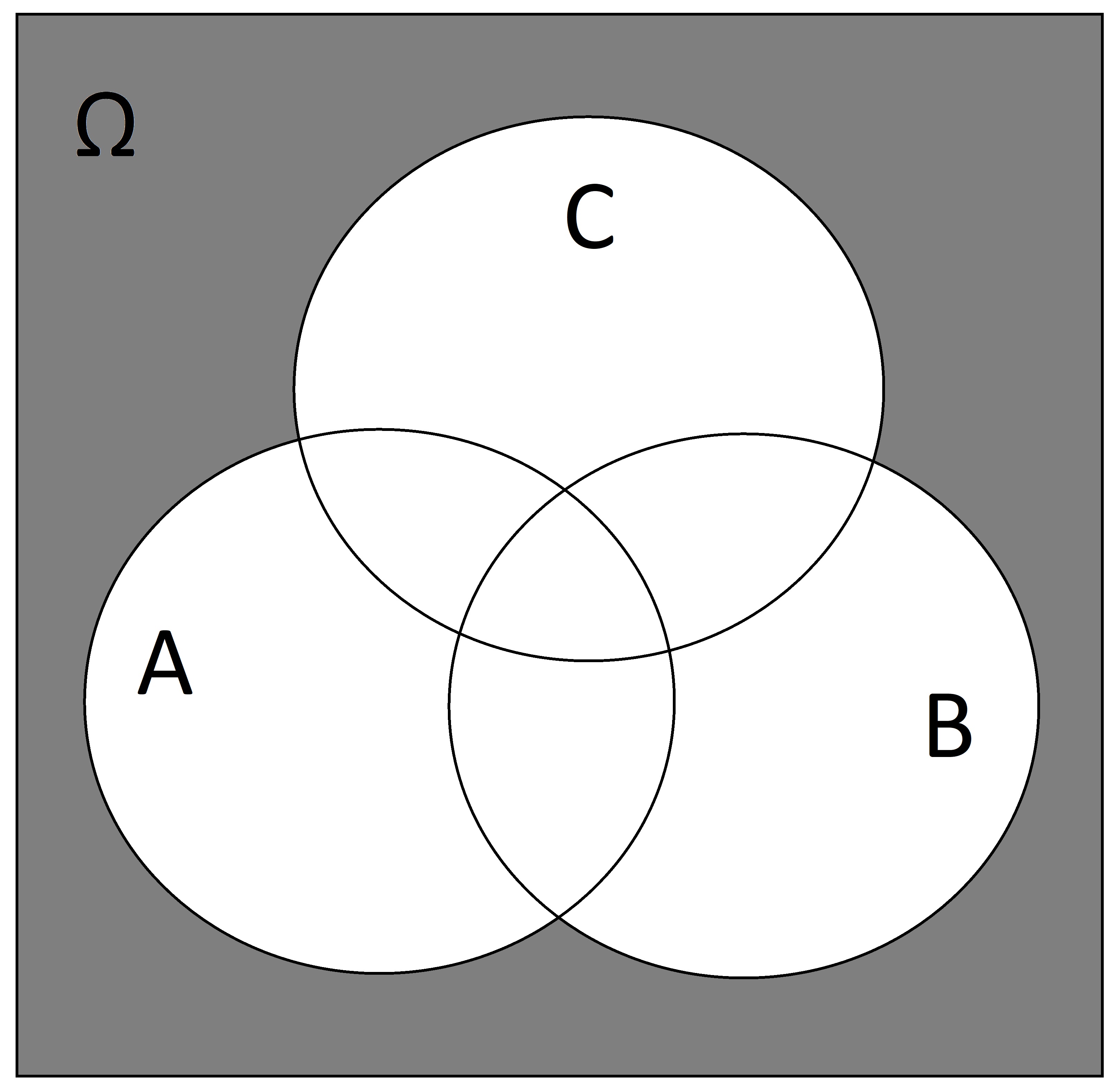
Shade in \((B \cup C) \setminus A\)

SOLUTION:
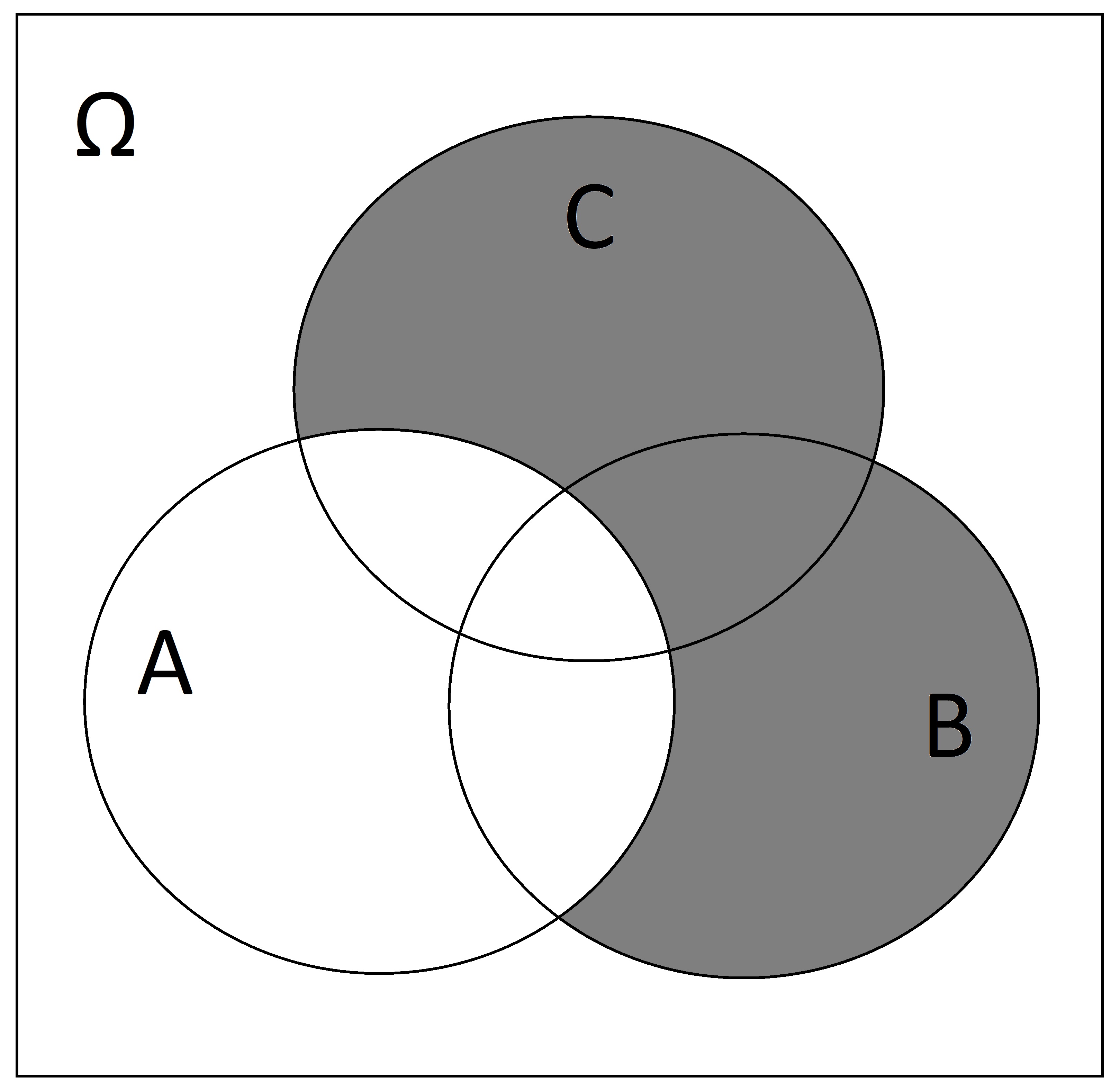
Shade in \(\overline{A \cap B \cap C}\)

SOLUTION:
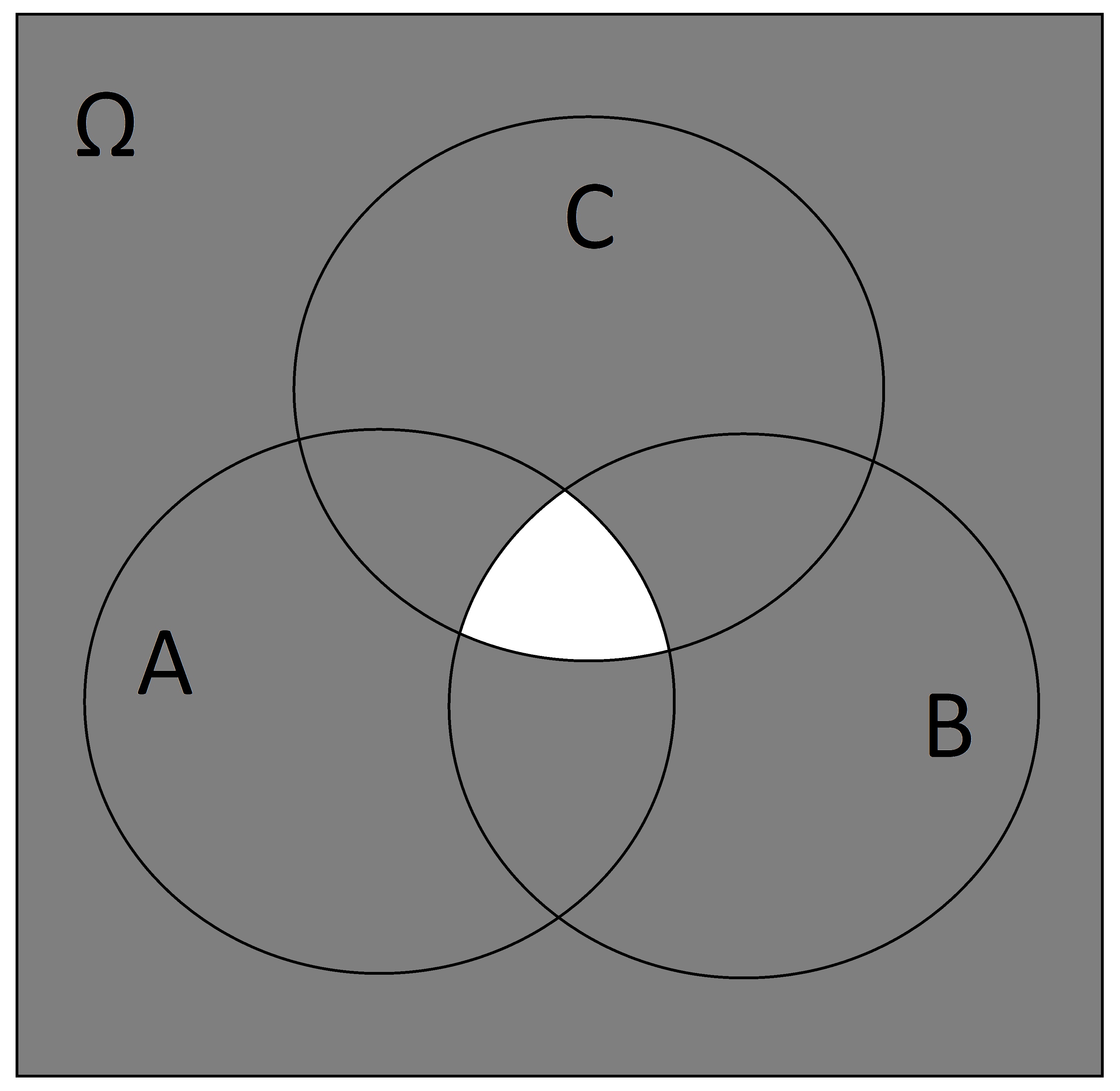
Shade in \(C \cap (A \cup B)\)

SOLUTION:

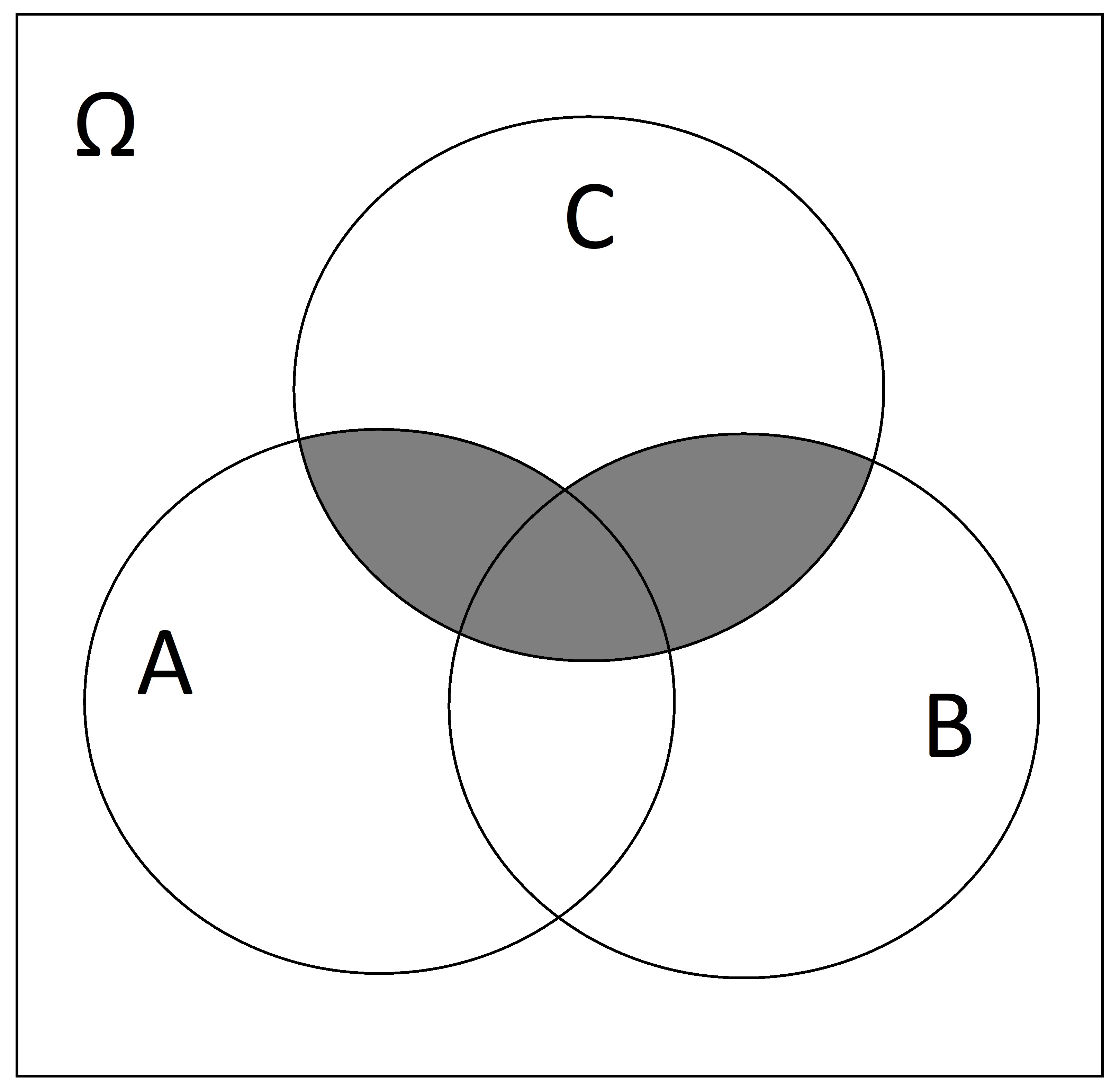
Question C

If \(\lvert A \rvert = 20\), \(\lvert B \rvert = 15\), and \(\lvert A \cup B \rvert = 35\), are \(A\) and \(B\) mutually exclusive? Explain why.

SOLUTION: If \(A\) and \(B\) are mutually exclusive then \(\lvert A \cap B \rvert = 0\), there are no elements that belong to both sets. We know that \(\lvert A \cup B\rvert = \lvert A \rvert + \lvert B \rvert - \lvert A \cap B \rvert\), subsitituting in we get \(35 = 20 + 15 - \lvert A \cap B \rvert\), ans solving we get \(\lvert A \cap B \rvert = 0\). Therefore \(A\) and \(B\) are mutually exclusive.
In a group of 100 people, 89 can speak English, and 33 can speak Welsh. Everyone can speak either English or Welsh. How many people speak both languages? How many speak English only?

SOLUTION:
- Let \(E\) be the set of people who can speak English, let \(W\) be the set of people who can speak Welsh. We know that \(\lvert E \rvert = 89\), \(\lvert W \rvert = 33\), and \(\lvert E \cup W\rvert = 100\).
- \(W \cap E\) is the set of people who can speak both languages. \(\lvert W \cap E\rvert = \lvert E \rvert + \lvert W \rvert - \lvert E \cup W \rvert\), so \(\lvert W \cap E\rvert = 89 + 33 - 100 = 22\).
- \(E \setminus W\) is the set of people who can speak English only. \(\lvert E \setminus W \rvert = \lvert E \rvert - \lvert E \cap W\), so \(\lvert E \setminus W \rvert = 89 - 22 = 67\).

Question D

Write down the sets represented by the following Venn diagrams:

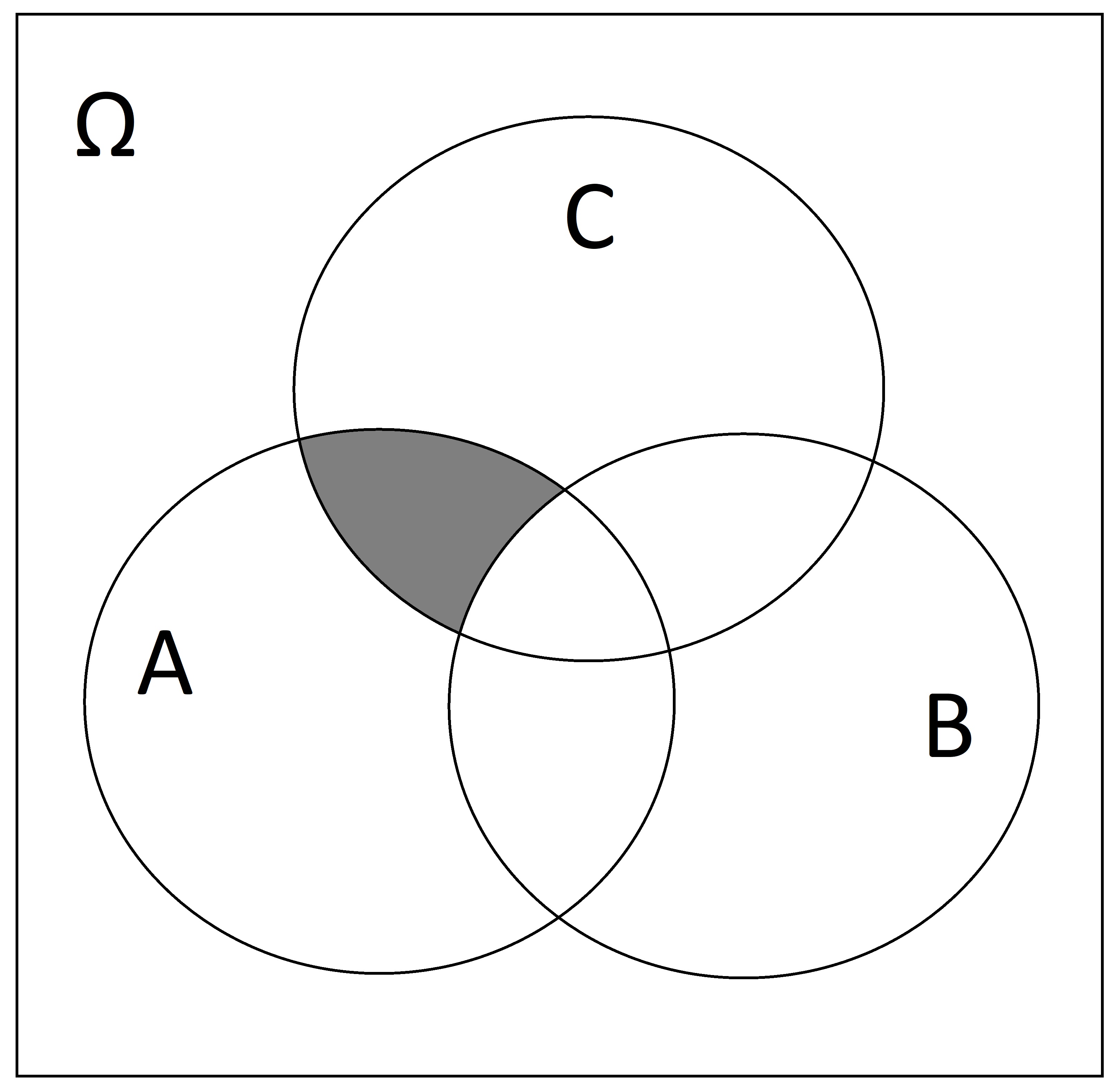
SOLUTION: \((A \cap C) \setminus B\) or alternatively \(A \cap C \cap \overline{B}\)
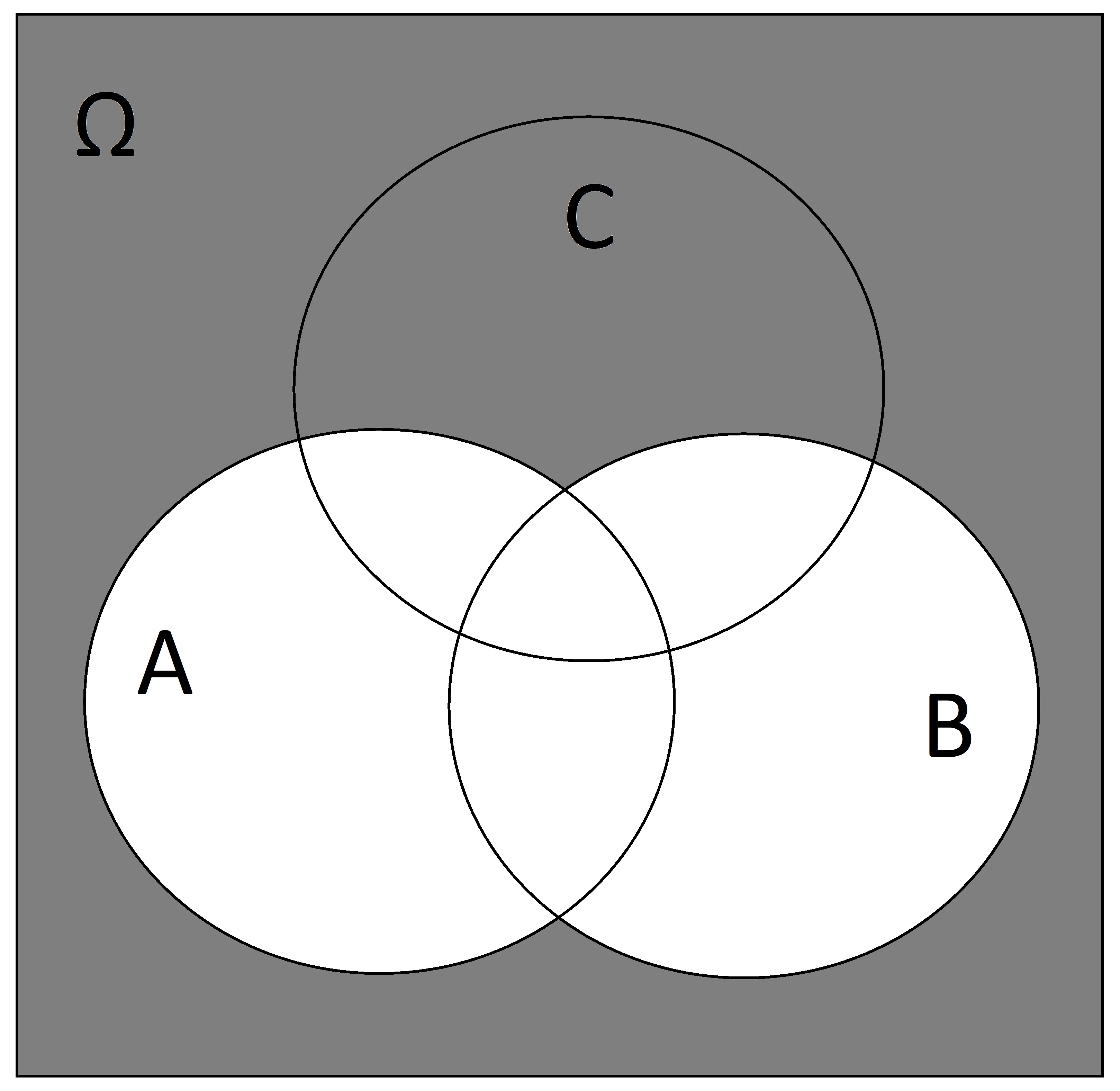
SOLUTION: \(\overline{A \cup B}\)
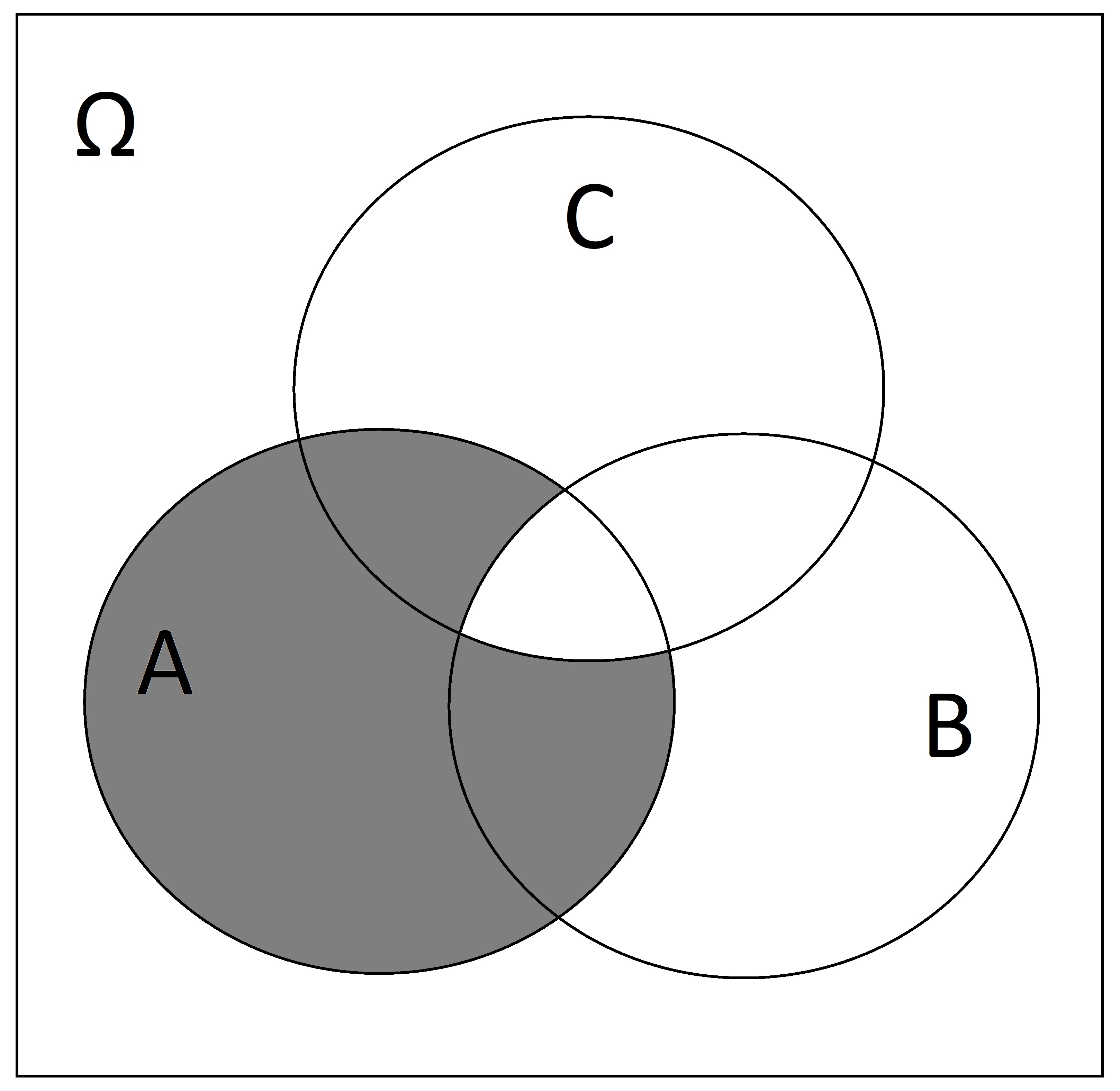
SOLUTION: \(A \setminus (B \cap C)\) or alternatively \(A \cap (\overline{B \cap C})\)
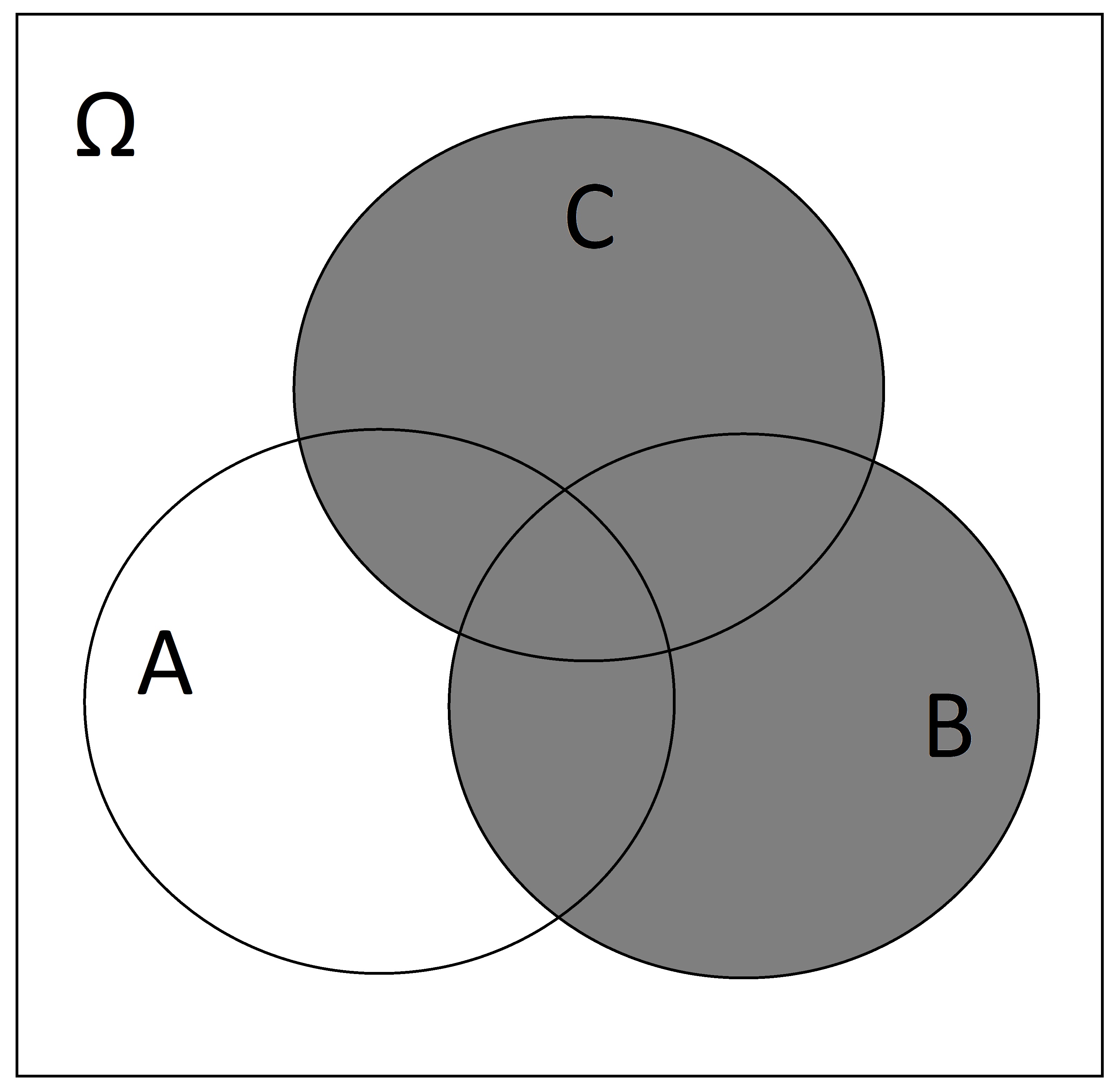
SOLUTION: \(B \cup C\)
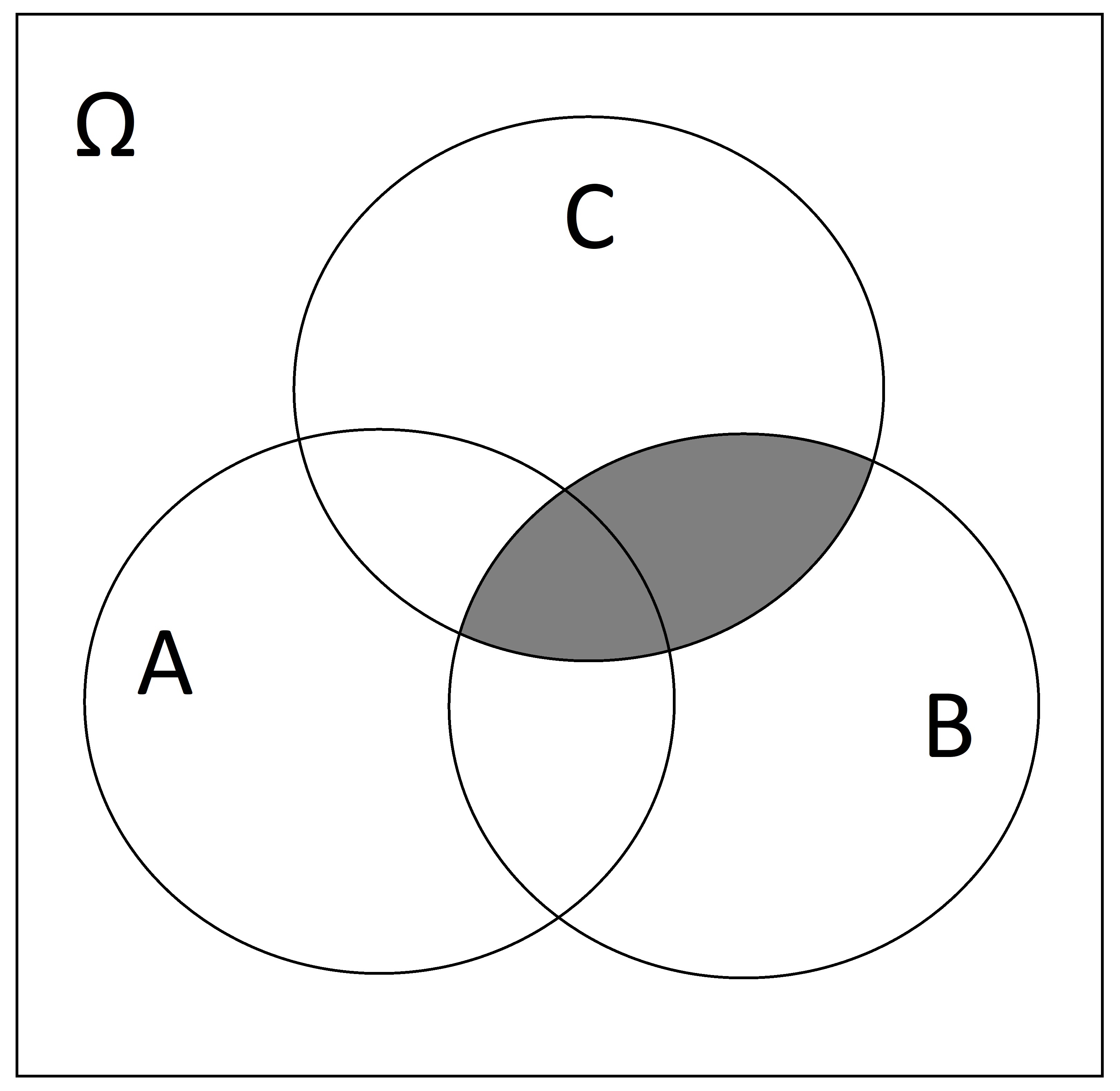
SOLUTION: \(B \cap C\)
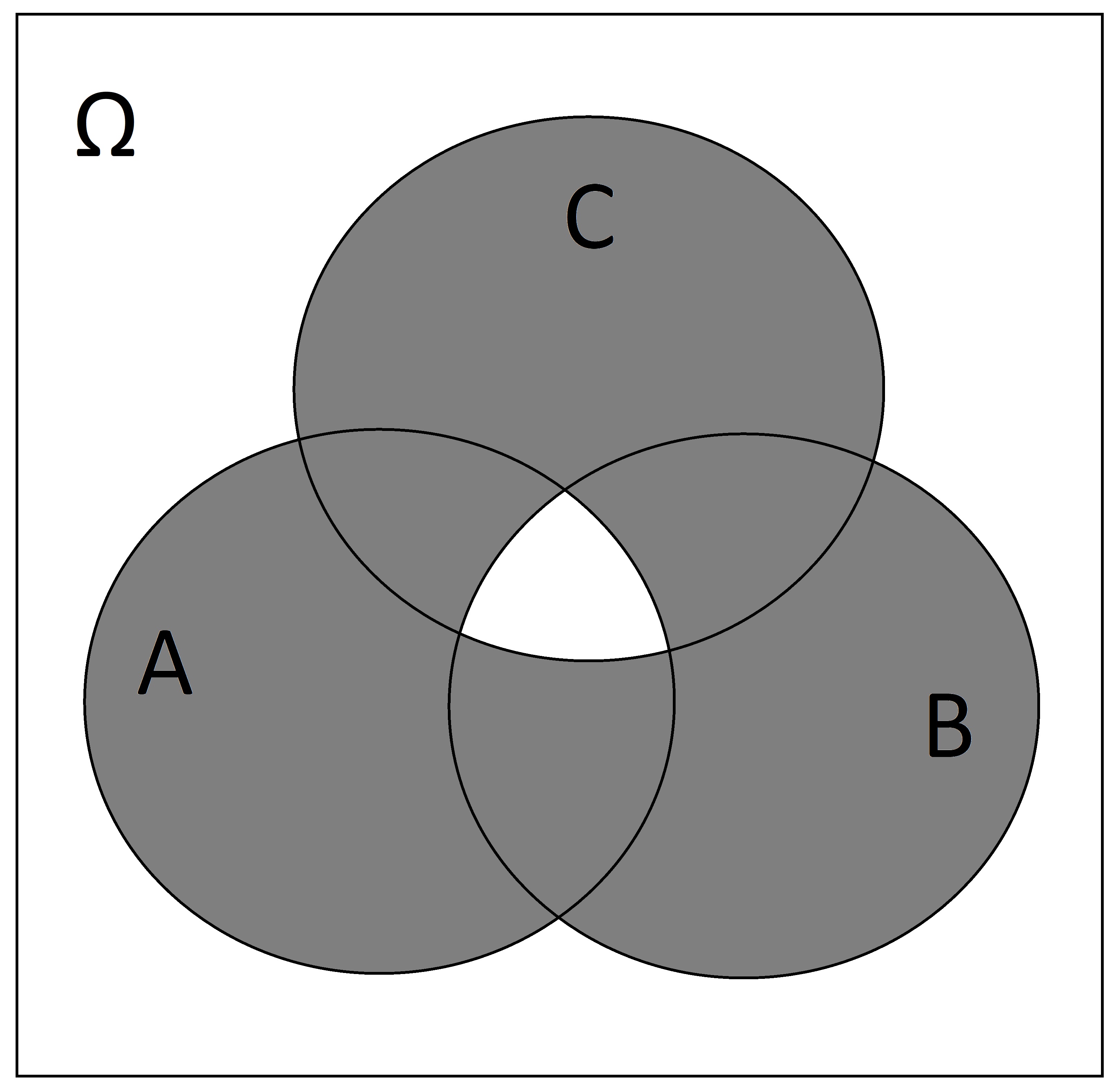
SOLUTION: \((A \cup B \cap C) \setminus (A \cap B \cap C)\) or alternatively \((A \cup B \cup C) \cap \overline{A \cap B \cap C}\)

Question E

Consider \(A\) and \(B\) to be general non-empty sets, and the universal set to be \(\Omega\). State whether the following statements are true or false.

If \(A \subset B\) then \(A \cap B = \emptyset\).

SOLUTION: False. If \(A \subset B\) and both are non-empty, then everything in \(A\) must also be in \(B\), and so \(A \cap B = B\).
It is true that \(A \cup B = B \cup A\)

SOLUTION: True. The \(\cup\) operator is communtative.
It is true that \(A \cap B = B \cap A\)

SOLUTION: True. The \(\cap\) operator is communtative.
\(P(A) \in A\), where \(P(A)\) is the power set of \(A\).

SOLUTION: False. This is only true is \(A = \emptyset\), and we have assumed that \(A\) is non-empty. However it is true the \(A \in P(A)\).
If \(A\) is finite and \(B\) is infinite, then \(A \cup B\) is infinite.

SOLUTION: True. Every element in \(B\) is also an element of \(A \cup B\), and so if \(B\) has an infinite amount of elements, so much \(A \cup B\).
If \(x \in A\) and \(y \in A\), then \(x = y\).

SOLUTION: False. \(A\) can contain more than one element.
If \(A\) and \(B\) are form a partition over \(\Omega\), then \(B = \overline{A}\).

SOLUTION: True. If \(A\) and \(B\) form a partition over \(\Omega\), then they are mutually exclusive, and every element must be either an element of \(A\) or \(B\). Let \(x \in B\), we know then that \(x \notin A\), and so \(x \in \overline{A}\). This is true for every such \(x\), and so \(B = \overline{A}\).
If \(A\) and \(B\) are mutually exclusive then \(A \cup B = \emptyset\).

SOLUTION: False. As either \(A\) or \(B\) are non-empty, then \(A \cup B\) cannot be empty. However, if \(A\) and \(B\) are mutually exclusive then \(A \cap B = \emptyset\).
\(\lvert A \setminus B \rvert = \lvert B \setminus A \rvert\).

SOLUTION: False. This can be shown by a contradition, let \(A = \{a, b, c\}\) and \(B = \{a, d\}\). Then \(A \setminus B = \{b, c\}\), so \(\lvert A \setminus B \rvert = 2\); and \(B \setminus A = \{d\}\), so \(\lvert B \setminus A \rvert = 1\).
If \(A \subset B\) then \(A \cup B = B\).

SOLUTION: True. If \(A \subset B\) then every element of \(A\) is also an element of \(B\). Let \(x \in A \cup B\). Now either \(x \in A\) or \(x \in B\). If \(x \in A\), then \(x \in B\) because \(A \subset B\). Therefore every element of \(A \cup B\) must be an element of \(B\), so \(A \cup B = B\).