Question A

State the following probabilities:

1. The probability of getting a heads when tossing a fair coin.

   SOLUTION: \(\mathbb{P}(\text{heads}) = \frac{1}{2}\) from the equally likely principle.

2. The probability of drawing a red card in a shuffled deck.

   SOLUTION: \(\mathbb{P}(\text{red card}) = \frac{26}{52} = \frac{1}{2}\) from the equally likely principle.

3. The probability of drawing the eight of clubs in a shuffled deck.

   SOLUTION: \(\mathbb{P}(\text{8 of clubs}) = \frac{1}{52}\) from the equally likely principle.

4. The probability of rolling snake’s eyes (two 1’s) when rolling a pair of dice.

   SOLUTION: \(\mathbb{P}(\text{snakes' eyes}) = \frac{1}{36}\) from the equally likely principle.

   Alternatively \(\mathbb{P}(\text{snakes' eyes}) = \mathbb{P}(\text{1 on first})\mathbb{P}(\text{1 on second}) = \frac{1}{6} \times \frac{1}{6} = \frac{1}{36}\) by considering sequences of independent events.

5. The probability of drawing an even heart or and odd club in a shuffled deck.

   SOLUTION: \(\mathbb{P}(\text{ever heart or odd club}) = \mathbb{P}(\text{even heart}) + \mathbb{P}(\text{odd club}) = \frac{5}{52} + \frac{5}{52} = \frac{10}{52} = \frac{5}{26}\) from the equally likely principle, and summing probabilities of mutually exclusive events.

6. The probability winning a four ball lottery (balls numbered from 1 to 59).

   SOLUTION:

   • If order matters, then: \(\mathbb{P}(\text{win lottery})\)
     \(= \mathbb{P}(\text{1st correct}) \mathbb{P}(\text{2nd correct } \vert \text{ 1st correct}) \mathbb{P}(\text{3rd correct } \vert \text{ rest correct}) \mathbb{P}(\text{4th correct } \vert \text{ rest correct})\)
     \(=\frac{1}{59} \times \frac{1}{58} \times \frac{1}{57} \times \frac{1}{56} = \frac{1}{10923024}\)
   • If order doesn’t matter then: \(\mathbb{P}(\text{win lottery})\)
     \(=\mathbb{P}(\text{1st from choice}) \mathbb{P}(\text{2nd from remaining } \vert \text{ 1st correct}) \mathbb{P}(\text{3rd from remaining } \vert \text{ rest correct}) \mathbb{P}(\text{4th from remaining } \vert \text{ rest correct})\)
     \(=\frac{4}{59} \times \frac{3}{58} \times \frac{2}{57} \times \frac{1}{56} = \frac{24}{10923024} = \frac{1}{455126}\)

Question B

Three drugs are to be tested on a group of 500 people, they are administered randomly as follows:

• On the first month half the population is chosen randomly to be given drug A.
• On the second month 130 people are chosen randomly to be given drug B.
• On the third month 40% of those people not given drug A are chosen randomly to be given drug C.

1. Draw a tree diagram of this.

   SOLUTION:

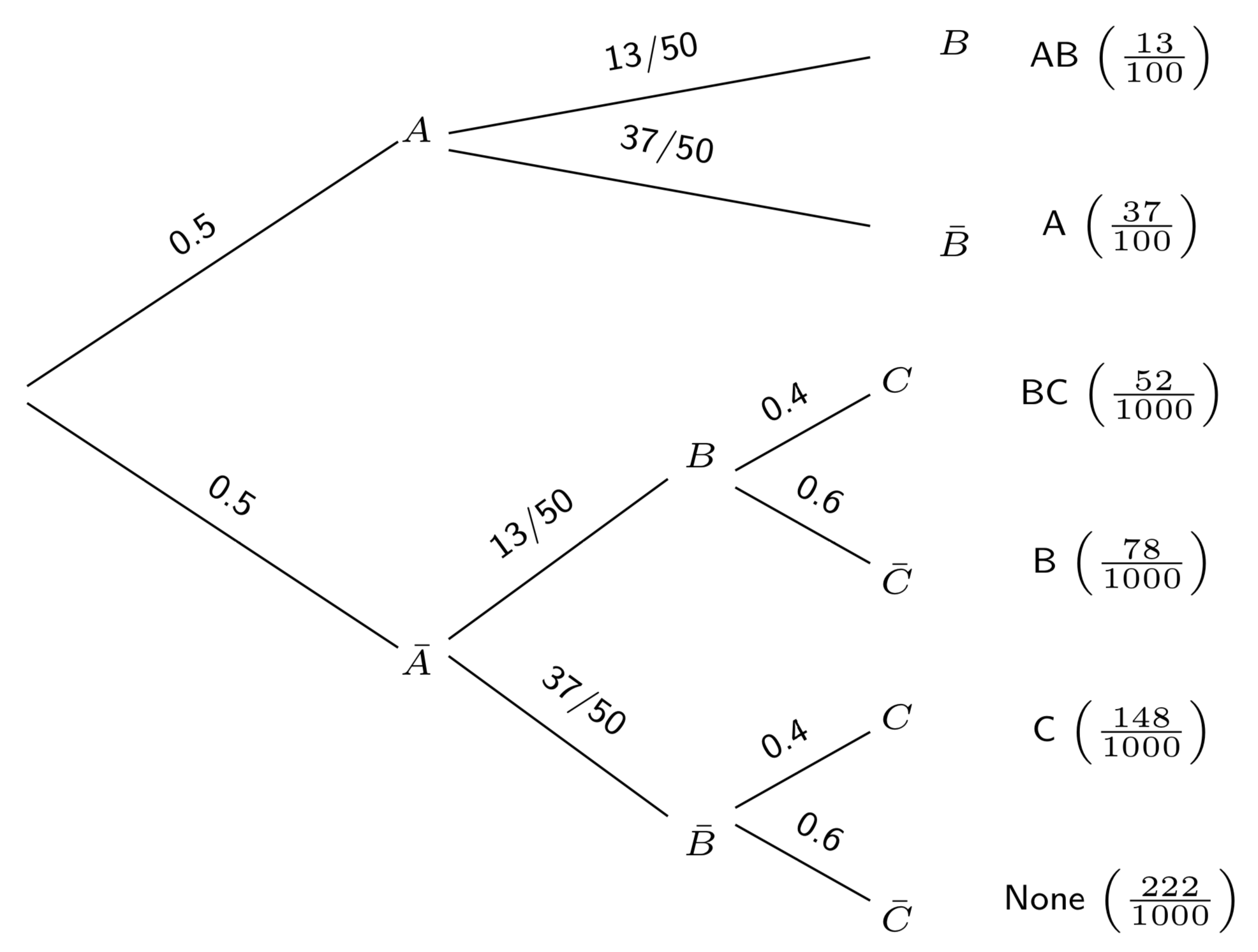
2. What is the probability of being given drug C?

   SOLUTION: \(\mathbb{P}(C) = \mathbb{P}\left(C \vert B \cap \overline{A}\right) \mathbb{P}\left(B \vert \overline{A}\right) \mathbb{P}\left(\overline{A}\right) + \mathbb{P}\left(C \vert \overline{B} \cap \overline{A}\right) \mathbb{P}\left(\overline{B} \vert \overline{A}\right) \mathbb{P}\left(\overline{A}\right) = \frac{52}{1000} + \frac{148}{1000} = \frac{200}{1000} = \frac{1}{5}\).

3. What is the probability of being given both drug A and B?

   SOLUTION: \(\mathbb{P}(A \cap B) = \frac{13}{100}\).

4. What is the probability of not receiving any drug at all?

   SOLUTION: \(\mathbb{P}\left(\overline{A} \cap \overline{B} \cap \overline{C}\right) = \frac{222}{1000} = \frac{111}{500}\).

Question C

Two events \(A\) and \(B\) have probability \(\mathbb{P}(A) = \frac{1}{6}\) and \(\mathbb{P}(B) = \frac{1}{2}\) of occurring, and \(\mathbb{P}(A \cap B) = \frac{2}{15}\).

1. Find \(\mathbb{P}\left(\overline{A}\right)\)

   SOLUTION: \(\mathbb{P}\left(\overline{A}\right) = 1 - \mathbb{P}(A) = 1 - \frac{1}{6} = \frac{5}{6}\).

2. Find \(\mathbb{P}(A \cup B )\)

   SOLUTION: \(\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B) = \frac{1}{6} + \frac{1}{2} - \frac{2}{15} = \frac{8}{15}\),

3. Find \(\mathbb{P}\left(\overline{A} \cap B\right)\)

   SOLUTION: Either \(\mathbb{P}\left(\overline{A} \cap B\right) = \mathbb{P}(A \cup B) - \mathbb{P}(A) = \frac{8}{15} - \frac{1}{6} = \frac{11}{30}\).
   Or: \(\mathbb{P}\left(\overline{A} \cap B\right) = \mathbb{P}(B) - \mathbb{P}(A \cap B) = \frac{1}{2} - \frac{2}{15} = \frac{11}{30}\).

4. Find the probability of \(A\) or \(B\) occurring, but not both.

   SOLUTION: \(\mathbb{P}\left(A \cap \overline{B}\right) + \mathbb{P}\left(\overline{A} \cap B\right) = \mathbb{P}(A) - \mathbb{P}(A \cap B) + \frac{11}{30} = \frac{1}{6} - \frac{2}{15} + \frac{11}{30} = \frac{6}{15}\).

Question D

In a certain card game only the Diamonds suit used (13 cards). You are dealt 2 cards. What is the probability of:

1. Getting a King?

   SOLUTION: \(\mathbb{P}(\text{king}) = \mathbb{P}(\text{king 1st}) + \left(\mathbb{P}(\text{no king 1st}) \mathbb{P}(\text{king 2nd } \mid \text{ no king 1st})\right) = \frac{1}{13} + \left(\frac{12}{13} \times \frac{1}{12}\right) = \frac{2}{13}\).

2. Getting a Queen and a Jack?

   SOLUTION: \(\mathbb{P}(Q \cup J) = \mathbb{P}(Q \text{ then } J) + \mathbb{P}(J \text{ then } Q) = \left(\frac{1}{13} \times \frac{1}{12}\right) + \left(\frac{1}{13} \times \frac{1}{12}\right) = \frac{1}{78}\)

3. Getting two cards that sum to 15? (face cards are not worth any points, aces are worth 1 point)

   SOLUTION: We saw in the previous question that the probability of getting exactly two specific cards is \(\frac{1}{78}\). The possibilities for summing to 15 are: 5 and 10, 6 and 9, and 7 and 8. So we want the probability of getting any of those combinations: \(\mathbb{P}(\text{sum to 15}) = \mathbb{P}(5 \cup 10)+\mathbb{P}(6 \cup 9)+ \mathbb{P}(7 \cup 8) = \frac{3}{78}\).

Question E

The government wants to know the proportion of people who have ever committed adultery. As this may be a potentially dangerous question to answer truthfully, the government anonymises the answer in the following manner: Participants are asked to roll two fair die, if both numbers are even must answer truthfully, otherwise they must lie. The die rolls are not recorded, so in this way there is no way for the anyone to find out who is lying. From 4000 replies, 2360 people say they have committed adultery. What is the true proportion of people who have committed adultery?

SOLUTION:

• Let \(T\) be the event that they tell the truth, and \(A\) be the event they say they are an adulterer.
• Now \(\mathbb{P}(T) = \mathbb{P}(\text{two even numbers}) = \mathbb{P}(\text{1st even})\mathbb{P}(\text{2nd even}) = \frac{1}{2} \times \frac{1}{2} = \frac{1}{4}\).
• Let \(x\) be the proportion of people who are adulterers. As being an adulterer and rolling two even numbers are independent events, draw the following tree diagram:

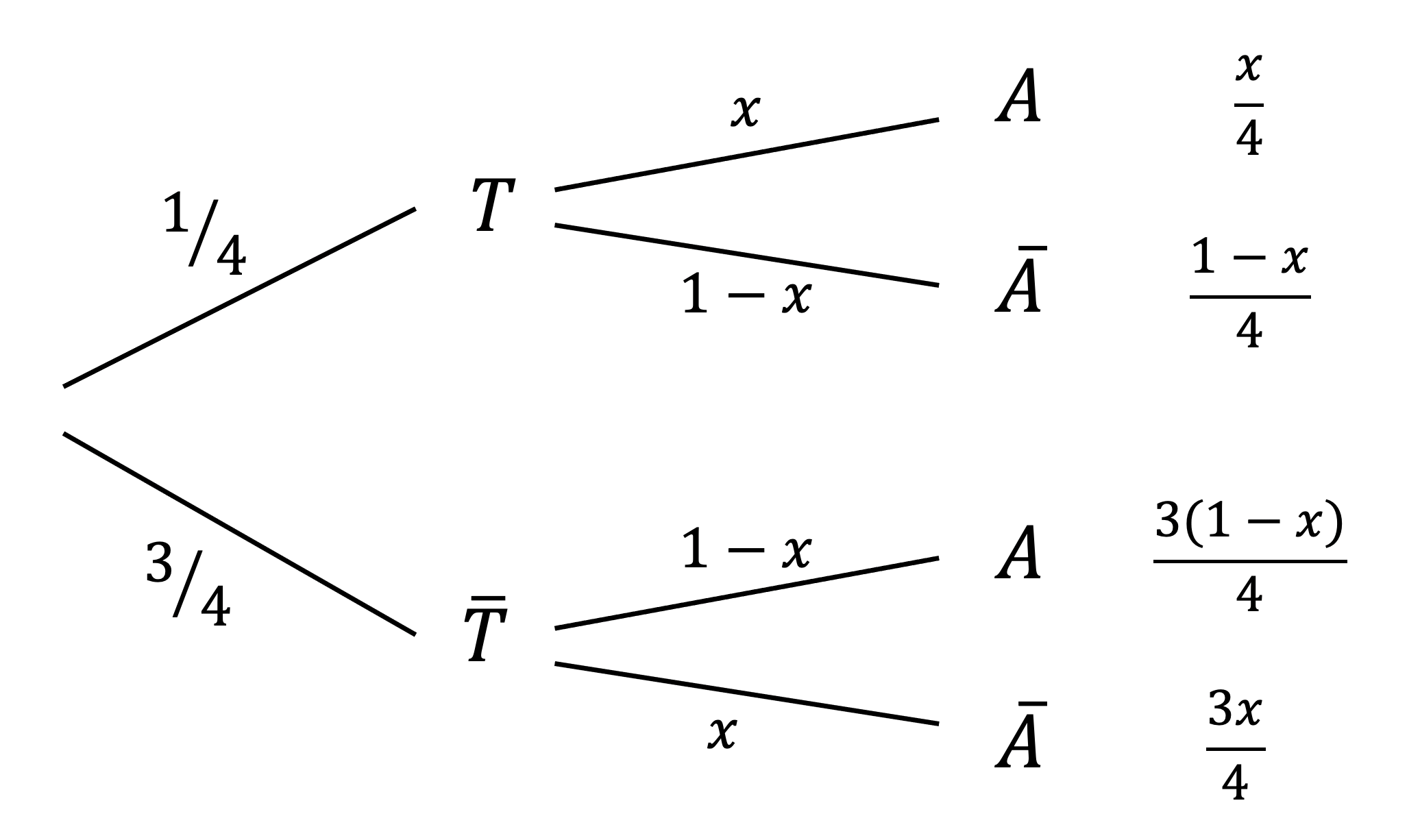
• We know that \(\mathbb{P}(A) = \frac{2360}{4000}\), and so from the tree diagram we get the equation: \(\frac{x}{4} + \frac{3(1-x)}{4} = \frac{2360}{4000}\).
• Solving gives \(x = \frac{8}{25}\).

Question F

Show whether the following pairs of events are independent or not:

1. “Drawing a heart” and “Drawing a red” from a shuffled deck of 52 cards (no jokers).

   SOLUTION: Let \(H\) be the event “drawing a heart”, and \(R\) be the event “drawing a red”.

   • If \(H\) and \(R\) are independent then \(\mathbb{P}(H \cap R) = \mathbb{P}(H)\mathbb{P}(R)\),
   • Now \(\mathbb{P}(H) = \frac{13}{52} = \frac{1}{4}\) by the equally likely principle,
   • similarly \(\mathbb{P}(R) = \frac{26}{52} = \frac{1}{2}\) by the equally likely principle,
   • and \(\mathbb{P}(H \cap R) = \frac{13}{52} = \frac{1}{4}\) by the equally likely principle.
   • Therefore \(\mathbb{P}(H \cap R) = \frac{1}{4} \neq \frac{1}{8} = \frac{1}{4}\times\frac{1}{2} = \mathbb{P}(H)\mathbb{P}(R)\), and so \(H\) and \(R\) are not independent events.

2. “Drawing an 8” and “Drawing a spade” from a shuffled deck of 52 cards (no jokers).

   SOLUTION: Let \(E\) be the event “drawing a eight”, and \(S\) be the event “drawing a spade”.

   • If \(E\) and \(S\) are independent then \(\mathbb{P}(H \cap R) = \mathbb{P}(H)\mathbb{P}(R)\),
   • Now \(\mathbb{P}(E) = \frac{4}{52} = \frac{1}{13}\) by the equally likely principle,
   • similarly \(\mathbb{P}(S) = \frac{13}{52} = \frac{1}{4}\) by the equally likely principle,
   • and \(\mathbb{P}(E \cap S) = \frac{1}{52}\) by the equally likely principle.
   • Therefore \(\mathbb{P}(E \cap S) = \frac{1}{52} = \frac{1}{13}\times\frac{1}{4} = \mathbb{P}(E)\mathbb{P}(S)\), and so \(E\) and \(S\) are independent events.

Question G

In New York 46% of all teenagers own a skateboard and 36% of all teenagers own both a skateboard and roller blades. What is the probability that a teenager owns roller blades given that the teenager owns a skateboard?

SOLUTION:

• We know that \(\mathbb{P}(\text{skateboard}) = 0.46\),
• and that \(\mathbb{P}(\text{skateboard } \cap \text{ rollerblades}) = 0.36\).
• Using conditional probability we get that \(\mathbb{P}(\text{rollerblades} \mid \text{skateboard}) = \frac{\mathbb{P}(\text{skateboard } \cap \text{ rollerblades})}{\mathbb{P}(\text{skateboard})} = \frac{0.36}{0.46} = \frac{18}{23}\).

Question H

The most popular first name in the world is Muhammed. The most popular middle name in the word is James. The most popular surname in the word is Wang.

Explain why it would be uncommon to meet someone named Muhammed James Wang.

SOLUTION: The events “having first name Muhammed”, “having middle name James”, and having surname “Wang” are not independent events.

Question I

Consider three events \(X\), \(Y\) and \(Z\). It is known than \(X\) and \(Y\) are mutually exclusive, \(\mathbb{P}(X) = 0.25\), \(\mathbb{P}(Y) = 0.25\), and \(\mathbb{P}(Z) = 0.4\). It is also known than \(\mathbb{P}(X \cap Z) = 0.05\) and \(\mathbb{P}(Y \cap Z) = 0.01\).

1. Find \(\mathbb{P}(X \cap Y)\)

   SOLUTION: \(\mathbb{P}(X \cap Y) = 0\) as \(X\) and \(Y\) are mutually exclusive.

2. Find \(\mathbb{P}(X \cup Y)\)

   SOLUTION: \(\mathbb{P}(X \cup Y) = \mathbb{P}(X) + \mathbb{P}(Y) - \mathbb{P}(X \cap Y) = 0.25 + 0.25 - 0 = 0.5\).

3. Find \(\mathbb{P}(X \cap Y \cap Z)\)

   SOLUTION: \(\mathbb{P}(X \cap Y \cap Z) = 0\) as \(\mathbb{P}(X \cap Y) = 0\).

4. Find \(\mathbb{P}\left(X \cap \overline{Z}\right)\)

   SOLUTION: \(\mathbb{P}\left(X \cap \overline{Z}\right) = \mathbb{P}(X) - \mathbb{P}(X \cap Z) = 0.25 - 0.05 = 0.2\).

5. Find \(\mathbb{P}\left(\overline{X} \cap \overline{Y} \cap \overline{Z}\right)\)

   SOLUTION:

   \[\begin{align*} \mathbb{P}\left(\overline{X} \cap \overline{Y} \cap \overline{Z}\right) &= \mathbb{P}\left(\overline{X \cup Y \cup Z}\right)\\ &= 1 - \left(\mathbb{P}(X) + \mathbb{P}(Y) + \mathbb{P}(Z) - \mathbb{P}(X \cap Y) - \mathbb{P}(X \cap Z) - \mathbb{P}(Y \cap Z) + \mathbb{P}(X \cap Y \cap Z)\right)\\ &= 1 - (0.25 + 0.25 + 0.4 - 0 - 0.05 - 0.01 + 0)\\ &= 0.16 \end{align*}\]

6. Find \(\begin{equation*}\mathbb{P}(X \mid Z)\end{equation*}\)

   SOLUTION: \(\begin{equation}\mathbb{P}(X \mid Z) = \frac{\mathbb{P}(X \cap Z)}{\mathbb{P}(Z)} = \frac{0.05}{0.4} = 0.125\end{equation}\)

7. Find \(\mathbb{P}(Z \mid X)\)

   SOLUTION:

   • Either directly using conditional probability: \(\begin{equation}\mathbb{P}(Z \mid X) = \frac{\mathbb{P}(X \cap Z)}{\mathbb{P}(X)} = \frac{0.05}{0.25} = 0.2\end{equation}\)
   • Or using Bayes’ theorem: \(\begin{equation}\mathbb{P}(Z \mid X) = \frac{\mathbb{P}(X \mid Z)\mathbb{P}(Z)}{\mathbb{P}(X)} = \frac{0.125 \times 0.4}{0.25} = 0.2\end{equation}\)

8. Find \(\mathbb{P}(X \cup Y \cup Z)\)

   SOLUTION: \(\mathbb{P}(X \cup Y \cup Z) = 1 - \mathbb{P}\left(\overline{X \cup Y \cup Z}\right) = 1 - \mathbb{P}\left(\overline{X} \cap \overline{Y} \cap \overline{Z}\right) = 1 - 0.16 = 0.84\)

Question J

The Pokérus virus is rare, it affects 1 in 21,845 Pokémon. Nurse Joy can test for the virus, but only with 98% accuracy. Brock suspects his Geodude had Pokérus, and the test is positive. What is the probability that Brock’s Geodude actually has the Pokérus virus?

(Bonus - What assumptions have you made that are not met by the wording of the question?)

SOLUTION: Let \(V\) be the event Geodude has the virus, and let \(T\) be the event that Geodude tests positive for the virus. The probability that Geodude has the virus given that they tested positive is \(\mathbb{P}(D \mid T)\), so this is what we are looking for.

We know that:

• \(\mathbb{P}(V) = \frac{1}{21845}\) and \(\mathbb{P}(\overline{V}) = \frac{21844}{21845}\), from the rarity of the virus.
• \(\mathbb{P}(T \mid V) = 0.98\), \(\mathbb{P}\left(\overline{T} \mid V\right) = 0.02\), \(\mathbb{P}\left(T \mid \overline{V}\right) = 0.02\), and \(\mathbb{P}\left(\overline{T} \mid \overline{V}\right) = 0.98\), from the accuracy of the test.

From total probability, or as shown using tree diagrams, we can get:

Finally using Bayes’ Theorem we get:

BONUS: There are two assumptions:

• That the accuracy of the test applied to true positives and true negatives. This is not usually the case.
• It is assumed that the probability of Geodude having the virus before being tested is the same as the prevalence of the virus. That is that \(\mathbb{P}(T)\) is the same for every Pokémon. However “Brock suspects his Geodude had Pokérus” (e.g. Geodude may have symptoms), which would increase \(\mathbb{P}(T)\) for this particular Geodude.

Question K

Here is a well known problem: the problem of two liars: Andy and Beatrice both only tell the truth a third of the time. A wallet is stolen and Andy says that he did not steal the wallet. Beatrice then confirms this. What is the probability that Andy is actually telling the truth?

SOLUTION: Let \(T\) be the event that both Andy and Beatrice told the truth. Let \(L\) be the event that both Andy and Beatrice are lying. Note that \(\overline{T} \neq L\). Let \(E\) be the event that we saw, that both Andy and Beatrice agreed with one another.

• \(\mathbb{P}(T) = \mathbb{P}(\text{Andy tells the truth})\mathbb{P}(\text{Beatrice tells the truth}) = \frac{1}{3} \times \frac{1}{3} = \frac{1}{9}\).
• \(\mathbb{P}(L) = \mathbb{P}(\text{Andy lies})\mathbb{P}(\text{Beatrice lies}) = \frac{2}{3} \times \frac{2}{3} = \frac{4}{9}\).
• \(\mathbb{P}(E) = \mathbb{P}(T) + \mathbb{P}(L) = \frac{1}{9} + \frac{4}{9} = \frac{5}{9}\).

We know \(E\) occurred, so the only possibility for Andy telling the truth is \(T\). So we are looking for \(T \mid E\):

using the fact that \(T \subset E\) and so \(\mathbb{P}(T) = \mathbb{P}(T \cap E)\).