Question A

Consider the following game of wheel of fortune:

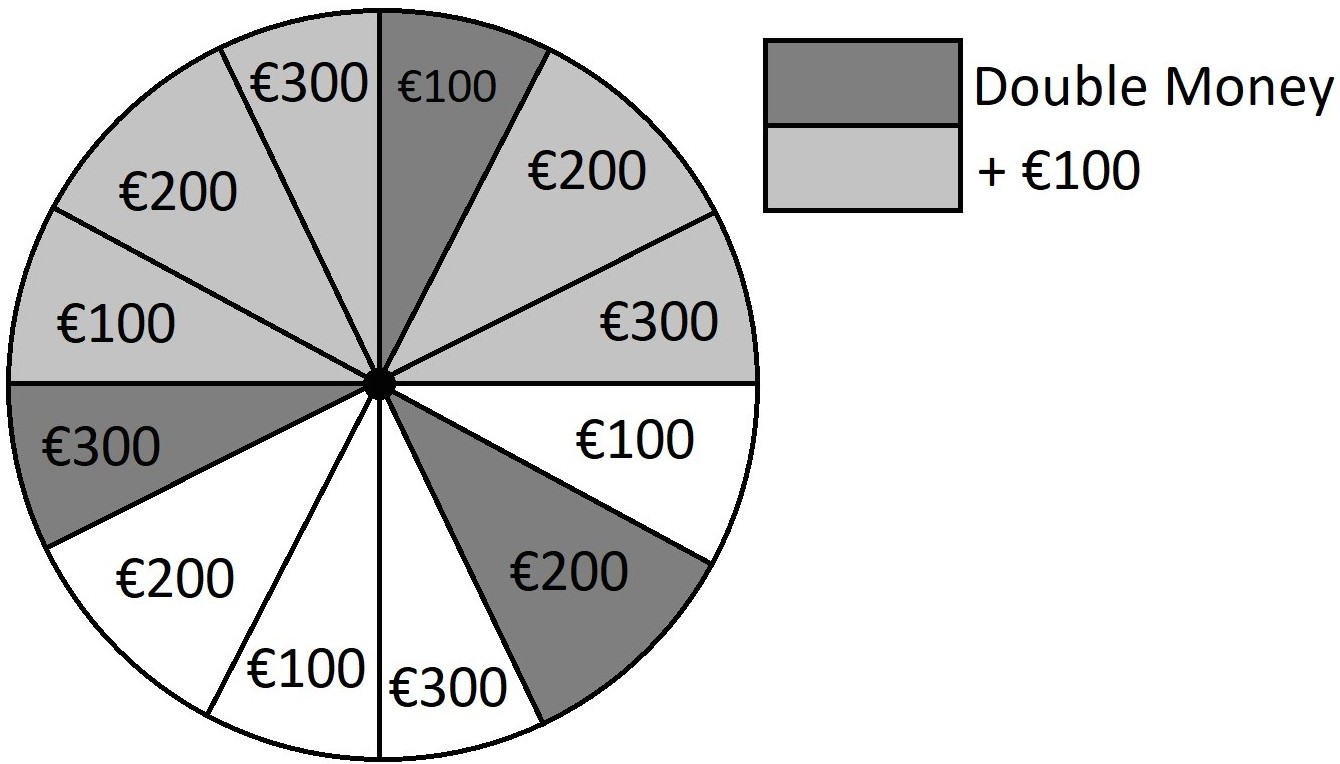
The wheel can land on each segment and they are equally likely. Players win the amount of money labelled on the segment, with the modifiers (+€100 or double money) on the corresponding coloured segments.

Write down the pmf and cdf of the outcome.

SOLUTION

\(x\)	€100	€200	€300	€400	€600
\(\mathbb{P}(X = x)\)	\(\frac{2}{12}\)	\(\frac{3}{12}\)	\(\frac{3}{12}\)	\(\frac{3}{12}\)	\(\frac{1}{12}\)
\(\mathbb{P}(X \leq x)\)	\(\frac{2}{12}\)	\(\frac{5}{12}\)	\(\frac{8}{12}\)	\(\frac{11}{12}\)	\(1\)

Calculate the expected outcome.

SOLUTION

Using the formula: \(\mathbb{E}(X) = \left(100 \times \frac{2}{12}\right) + \left(200 \times \frac{3}{12}\right) + \left(300 \times \frac{3}{12}\right) + \left(400 \times \frac{3}{12}\right) + \left(600 \times \frac{1}{12}\right) = \frac{3500}{12} = €291.66\).
Calculate the variance of the outcome.

SOLUTION

Using the formula:

\(\begin{align} Var(X) &= \left((100 - 291.66)^2 \times \frac{2}{12}\right) + \left((200 - 291.66)^2 \times \frac{3}{12}\right) + \left((300 - 291.66)^2 \times \frac{3}{12}\right)\\ &+ \left((400 - 291.66)^2 \times \frac{3}{12}\right) + \left((600 - 291.66)^2 \times \frac{1}{12}\right)\\ &= \frac{229166.66}{12} = €19097.22 \end{align}\).
What’s the most amount of money the casino can charge to spin the weel so that at least 30% of all players make a profit?

SOLUTION

30% of all players earn €400 or more. Therefore charging anything under €400 will result in 30% of players making a profit. Hence the most the casino can charge would be €399.99.
What is the mean profit?

SOLUTION

The mean winnings is €291.66. Charing €399.99 for the game would result in a mean outcome of €291.66 - €399.99 = -€108.33 for the player, hence a mean profit of €108.33 for the casino.
If each contestant played the game \(n\) times and the prizes cumulated, what would you expect the distribution of the outcome to be if \(n\) was very very large?

We would expect the distribution of the outcome to approach a Normal distribution as \(n\) got very large due to the central limit theorem.

Question B

Let X be the random variable representing the minimum value of two dice.

Write down the pmf of X.

SOLUTION

\(x\)	1	2	3	4	5	6
\(\mathbb{P}(X=x)\)	\(\frac{11}{36}\)	\(\frac{9}{36}\)	\(\frac{7}{36}\)	\(\frac{5}{36}\)	\(\frac{3}{36}\)	\(\frac{1}{36}\)

Calculate \(\mathbb{E}[X]\) and \(Var(X)\).

Using the formula: \(\mathbb{E}(X) = \left(1 \times \frac{11}{36}\right) + \left(2 \times \frac{9}{36}\right) + \left(3 \times \frac{7}{36}\right) + \left(4 \times \frac{5}{36}\right) + \left(5 \times \frac{3}{36}\right) + \left(6 \times \frac{1}{36}\right) = \frac{91}{36} = 2.527\)

Using the formula:

\(\begin{align} Var(X) &= \left((1 - 2.527)^2 \times \frac{11}{36}\right) + \left((2 - 2.527)^2 \times \frac{9}{36}\right) + \left((3 - 2.527)^2 \times \frac{7}{36}\right)\\ &+ \left((4 - 2.527)^2 \times \frac{5}{36}\right) + \left((5 - 2.527)^2 \times \frac{3}{36}\right) + \left((6 - 2.527)^2 \times \frac{1}{36}\right)\\&=1.9714 \end{align}\).
Find \(\mathbb{P}(X \leq 3)\).

SOLUTION

From the pmf:
\[\begin{align} \mathbb{P}(X \leq 3) &= \mathbb{P}(X = 1) + \mathbb{P}(X = 2) + \mathbb{P}(X = 3)\\ &= \frac{11}{36} + \frac{9}{36} + \frac{7}{36}\\ &= \frac{27}{36} = \frac{3}{4} \end{align}\]
If \(Y\) is the is the minimum value of \(n\) dice thrown at the same time, what would you expect the distribution of \(Y\) to be if \(n\) was very very large?

SOLUTION

As \(n\) gets very very large, the probability of getting a 1 on at least one die increases, and so the probability of the minimum being a 1 increases. So the larger \(n\) is, the pdf would be \(P(X = 1) = 1\).

The central limit theorem does not apply here because this is the minimum of \(n\) random variables, not the sum of \(n\) random variables.

Question C

It is known that the height of an appartment building in in Manhattan follows a Normal distribution, with mean 46.3m and standard deviation 10m. A building is chosen at random.

What is the probability that it is between 36.3m and 56.3m?

SOLUTION

This is the range of buildings withing 1 standard deviation from the mean, and for a Normal distribution we know that 68% of values lie within one standard deviation from the mean. Therefore the probability should be around 0.68.

We can calculate this exactly:
\[\begin{align} \mathbb{P}(36.3 \leq X \leq 56.3) &= \mathbb{P}\left(\frac{36.3-46.3}{10} \leq Z \leq \frac{56.3-46.3}{10}\right)\\ &= \mathbb{P}(-1 \leq Z \leq 1)\\ &= \mathbb{P}(Z \leq 1) - \mathbb{P}(Z \leq -1)\\ &= \mathbb{P}(Z \leq 1) - \mathbb{P}(Z \geq 1)\\ &= \mathbb{P}(Z \leq 1) - \left(1 - \mathbb{P}(Z \leq 1)\right)\\ &= 2\mathbb{P}(Z \leq 1) - 1\\ &= (2 \times 0.84134) - 1\\ &= 0.68268 \end{align}\]
What is the probability that it is taller than 63m?

SOLUTION
\[\begin{align} \mathbb{P}(X \geq 63) &= \mathbb{P}\left(Z \geq \frac{63-46.3}{10}\right)\\ &= \mathbb{P}(Z \geq 1.67)\\ &= 1 - \mathbb{P}(Z \leq 1.67)\\ &= 1 - 0.95254\\ &= 0.04746 \end{align}\]
What is the probability that it is shorter than 20m?

SOLUTION
\[\begin{align} \mathbb{P}(X \leq 20) &= \mathbb{P}\left(Z \leq \frac{20-46.3}{10}\right)\\ &= \mathbb{P}(Z \leq -2.63)\\ &= \mathbb{P}(Z \geq 2.63)\\ &= 1 - \mathbb{Z \leq 2.63} &= 1 - 0.99573\\ &= 0.00427 \end{align}\]
What is the probability that it is between 40m and 55m?

SOLUTION
\[\begin{align} \mathbb{P}(40 \leq X \leq 55) &= \mathbb{P}\left(\frac{40-46.3}{10} \leq Z \leq \frac{55-46.3}{10}\right)\\ &= \mathbb{P}(-0.63 \leq Z \leq 0.87)\\ &= \mathbb{P}(Z \leq 0.87) - \mathbb{P}(Z \leq -0.63)\\ &= \mathbb{P}(Z \leq 0.87) - \mathbb{P}(Z \geq 0.63)\\ &= \mathbb{P}(Z \leq 0.87) - \left(1 - \mathbb{P}(Z \leq 0.63)\right)\\ &= 0.80785 - (1 - 0.73565) &= 0.5435 \end{align}\]
What is the probability that it is taller than 70m or shorter than 10m?

SOLUTION

These two scenatios are mutually exclusive, so we can add their probabilities.
\[\begin{align} \mathbb{P}(X \geq 70) &= \mathbb{P}\left(Z \geq \frac{70-46.3}{10} \right)\\ &= \mathbb{P}(Z \geq 2.37)\\ &= 1 - \mathbb{P}(Z \leq 2.37)\\ &= 1 - 0.99111\\ &= 0.00889 \end{align}\]
and
\[\begin{align} \mathbb{P}(X \leq 10) &= \mathbb{P}\left(Z \leq \frac{10-46.3}{10} \right)\\ &= \mathbb{P}(Z \leq -3.63)\\ &= 0 \end{align}\]
this is so small to as be considered 0.

Therefore: \(\mathbb{P}((X \geq 70) \cup (X \leq 10)) = 0.00889 + 0 = 0.0889\)
If I choose a Manhattan resident at random, would I expect the mean height of their building to be 46.3m? Explain your answer.

SOLUTION

No. The taller the building, the more residents would live there. Therefore, choosing residents at random, we would be more likely to choose residents living in taller buildings than in shorter buildings. This is an example of inspection bias.
Give a reason why the height of Manhattan buildings cannot truly follow a Normal distribution.

SOLUTION

In a truly Normal distribution, there is possibility to have negative values. It is impossible to have a Manhattan building with negative height.

Question D

It is known that the price of artworks sold at an auction in 2019 was Normally distirbuted with mean £1300 and standard deviation £250.

Roughly what proportion of artworks were sold for more than £1300?

SOLUTION

Half the artworks sold for more than £1300. In a Normal distribution, the mean is equal to the median, and so 50% of values lie above the mean, and 50% of values lie below the mean.
Give the first and third quartiles of the distribution.

SOLUTION

Q1 = the price that 25% of the artworks sold less than. Q3 = the price that 75% of the artworks sold less than.

Let’s find a \(z_3\) value where \(\mathbb{P}(Z \leq z_3) = 0.75\), that is a value where 75% of \(Z\) values lie below it. Looking through the tables, we find that \(0.67 \leq z_3 \leq 0.68\), so let’s guess than \(z_3 = 0.675\).

Working backwards we find that \(X = \sigma z_3 + \mu = (250 \times 0.675) + 1300 = 1468.75\).

Therefore Q3 = £1468.75.

From symmetry, for Q1 we use \(z_1 = -z_3\), so \(X = \sigma z_1 + \mu = (250 \times -0.675) + 1300 = 1131.25\).

Therefore Q1 = £1131.25.
What proportion of artworks were sold for more than £1000?

SOLUTION
\[\begin{align} \mathbb{P}(X \geq 1000) &= \mathbb{P}\left(Z \geq \frac{1000-1300}{250} \right)\\ &= \mathbb{P}(Z \geq -1.2)\\ &= \mathbb{P}(Z \leq 1.2)\\ &= 0.88493 \end{align}\]
What proportion of artworks were sold for more than £2000?

SOLUTION
\[\begin{align} \mathbb{P}(X \geq 2000) &= \mathbb{P}\left(Z \geq \frac{2000-1300}{250} \right)\\ &= \mathbb{P}(Z \geq 2.8)\\ &= 0 \end{align}\]
this is so small to as be considered 0.