Question A

Consider the sets \(A = \{x, 7, 13\}\) and \(B = \{x, 2, 14, 15\}\).

Write down \(A \cup B\).
Write down \(A \cap B\).
Write down the power sets of \(A\) and \(B\).
Write down \(\lvert A \setminus B \rvert\)
Let \(C\) be the set of values that are impossible for \(x\) to take. Write down \(C\).

Question B

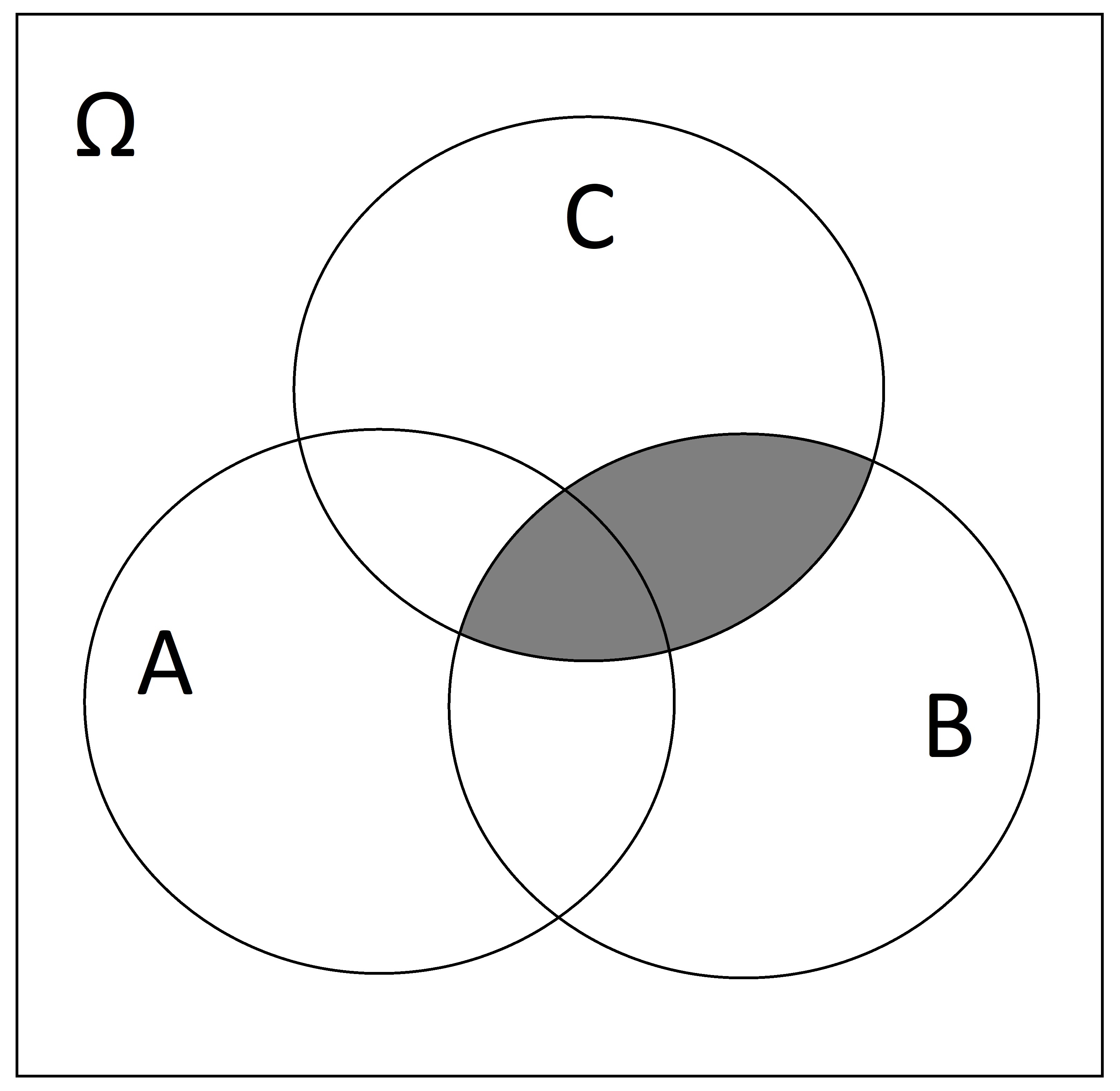
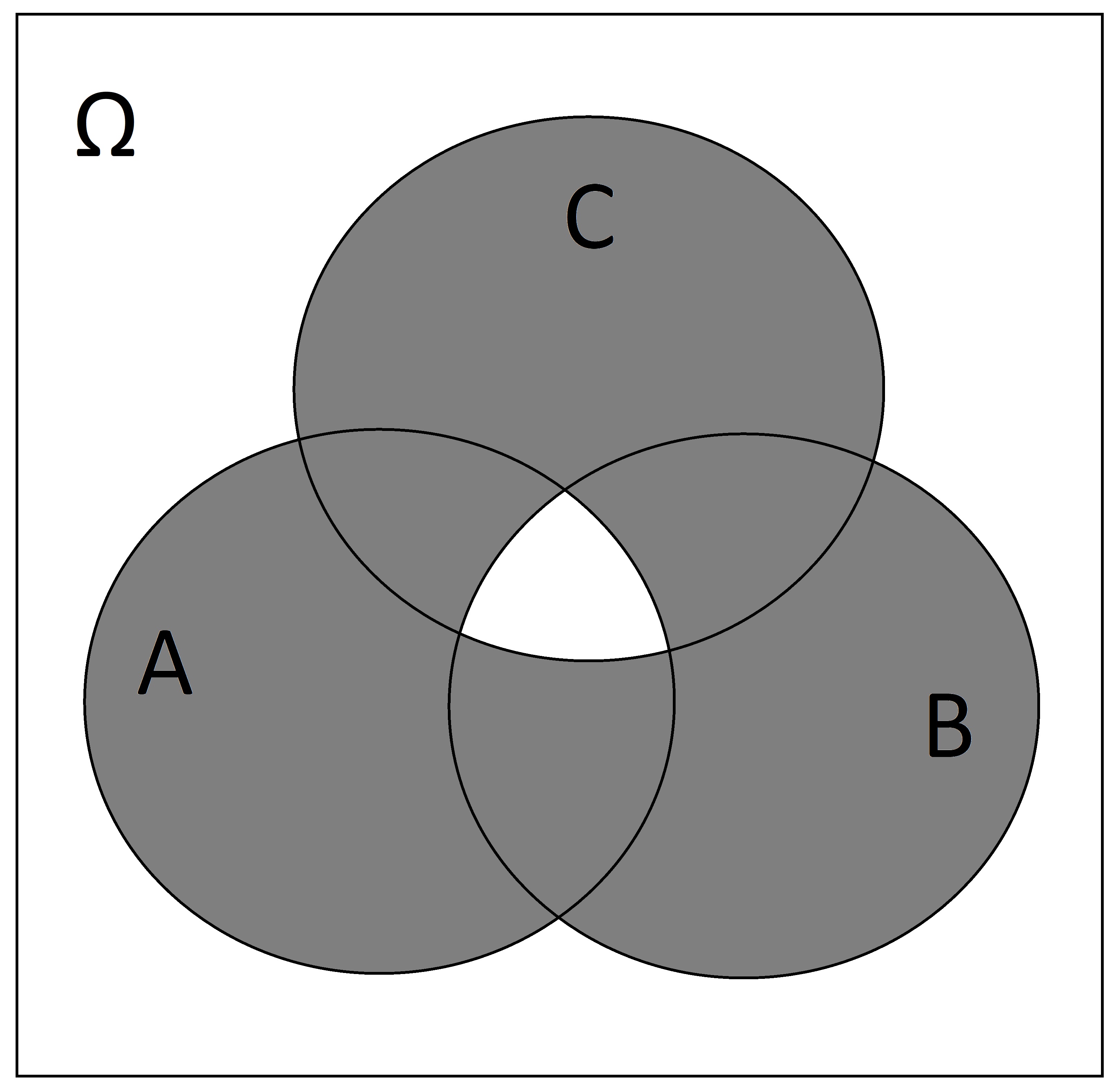
Consider the empty Venn diagram below:

Shade in \(A \cup B\)
Shade in \(A \cap C\)
Shade in \(\overline{A \cup B \cup C}\)
Shade in \((B \cup C) \setminus A\)
Shade in \(\overline{A \cap B \cap C}\)
Shade in \(C \cap (A \cup B)\)

Question C

If \(\lvert A \rvert = 20\), \(\lvert B \rvert = 15\), and \(\lvert A \cup B \rvert = 35\), are \(A\) and \(B\) mutually exclusive? Explain why.
In a group of 100 people, 89 can speak English, and 33 can speak Welsh. Everyone can speak either English or Welsh. How many people speak both languages? How many speak English only?

Question D

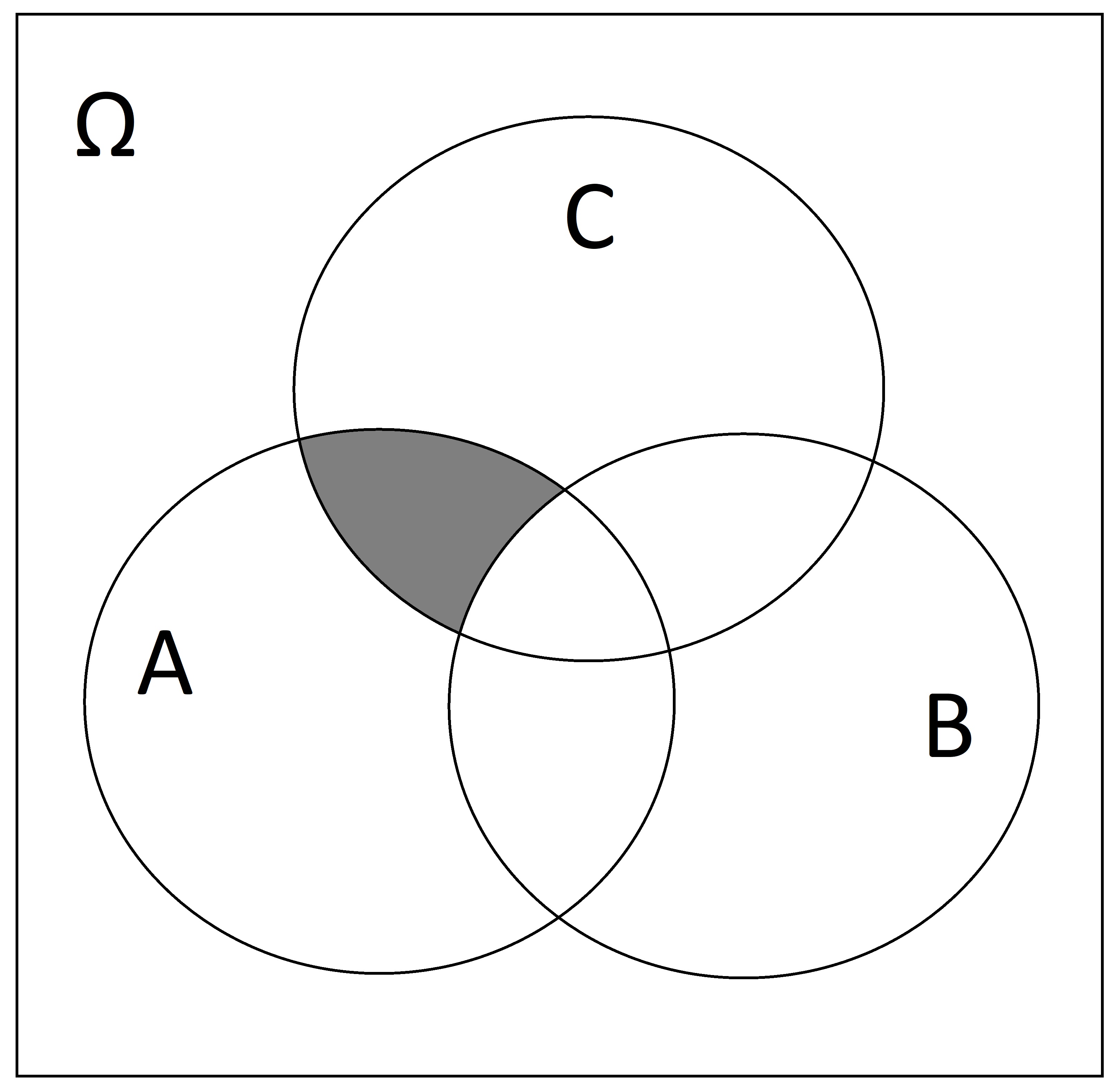
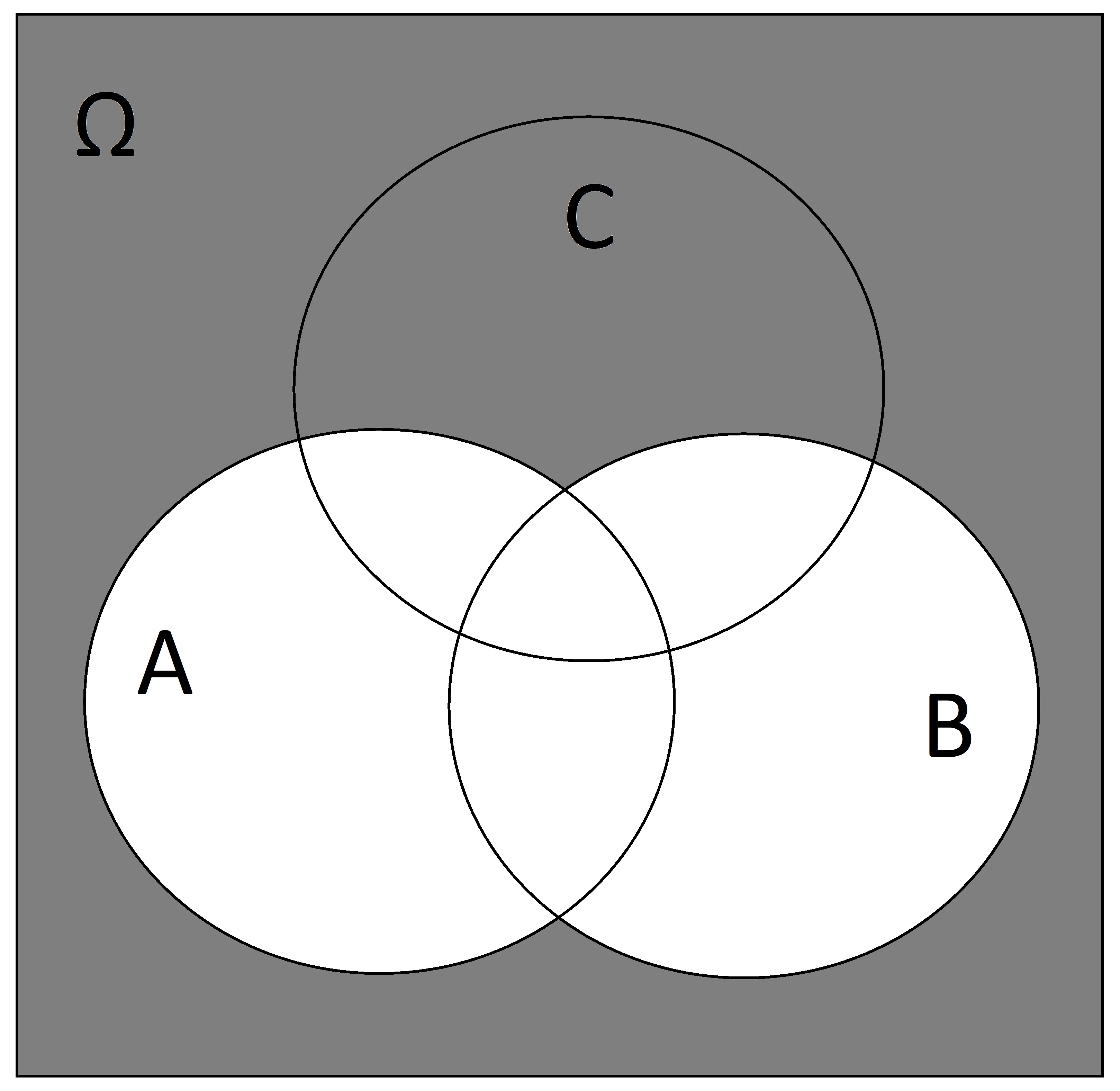
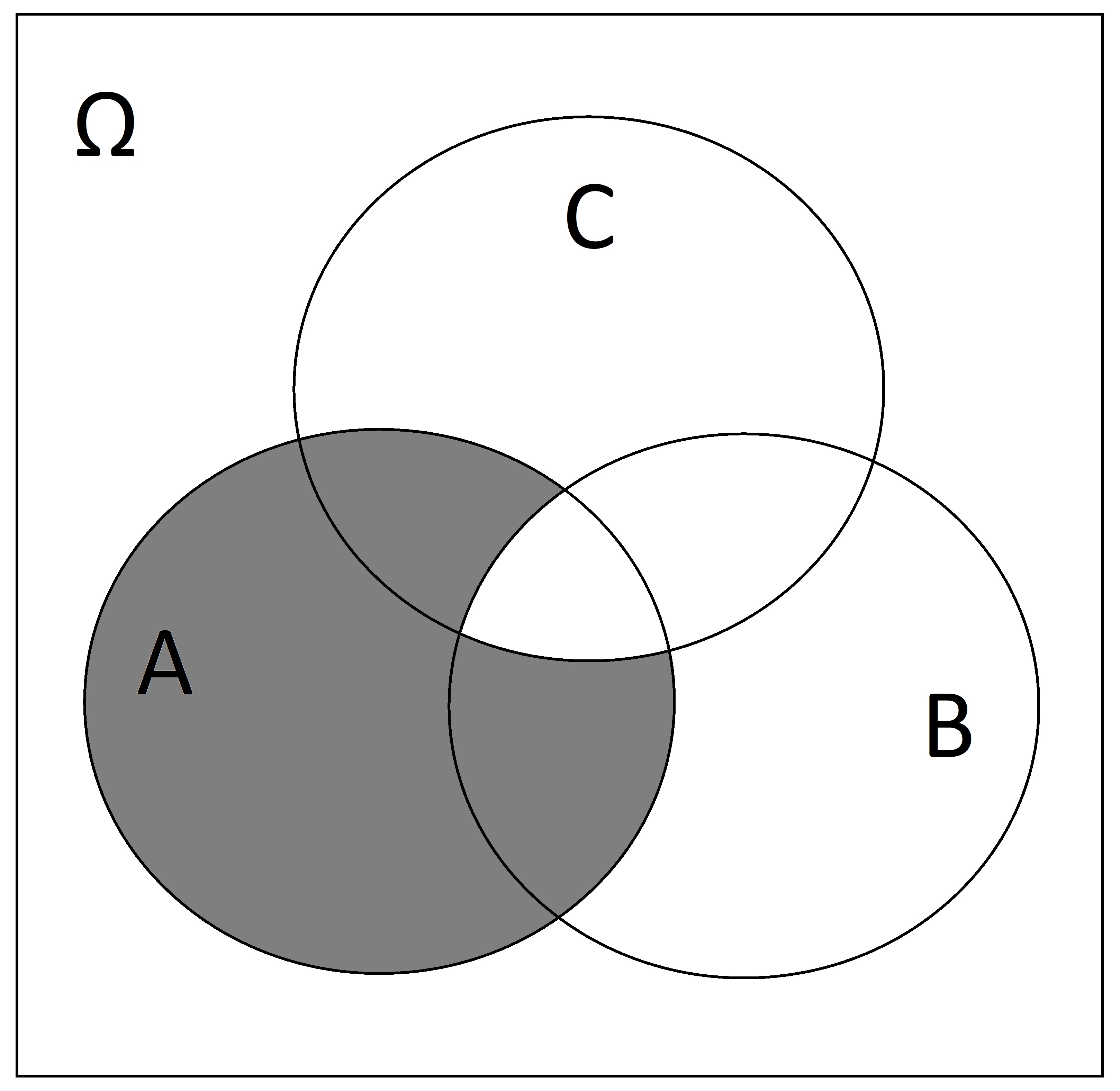
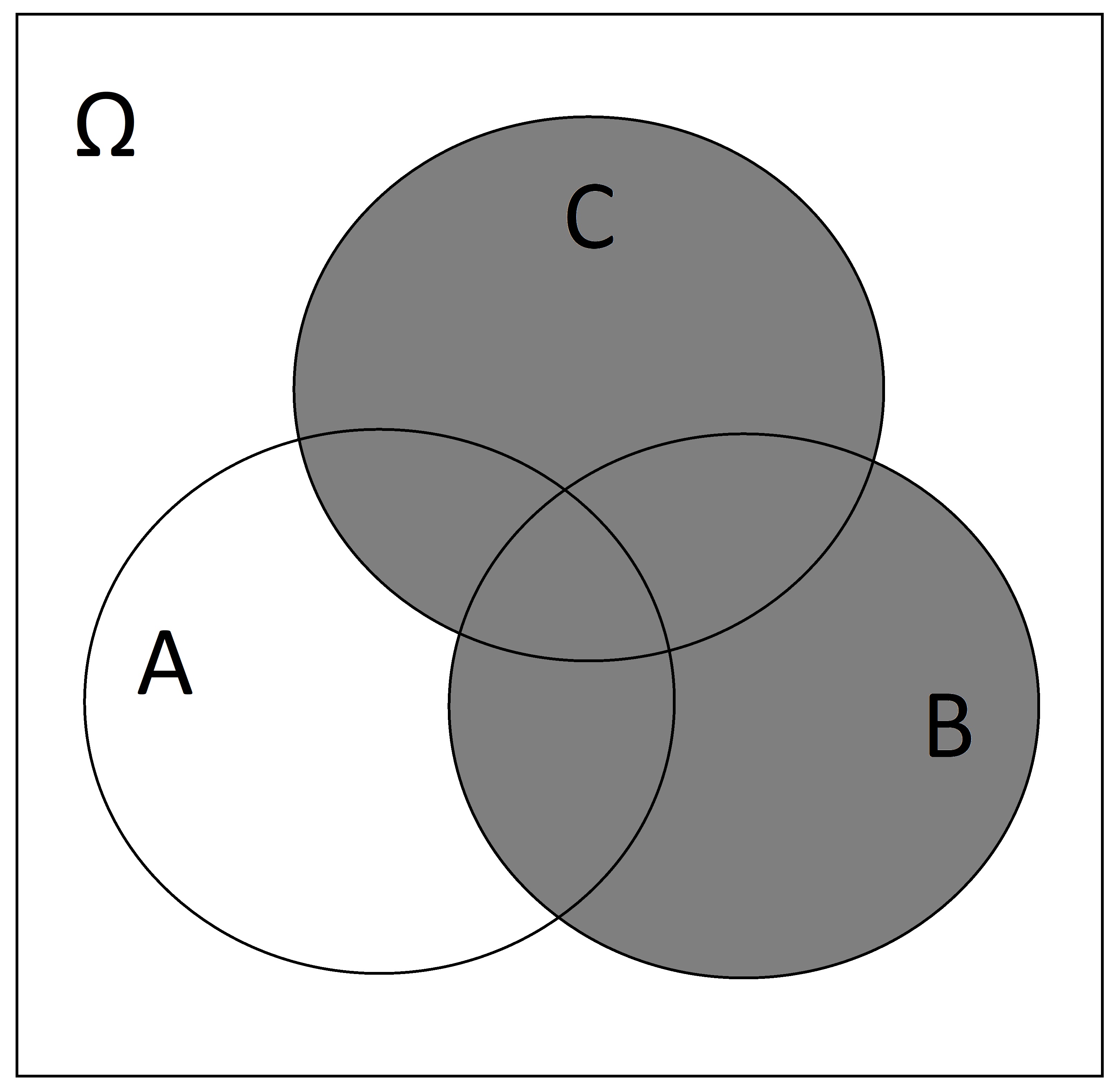
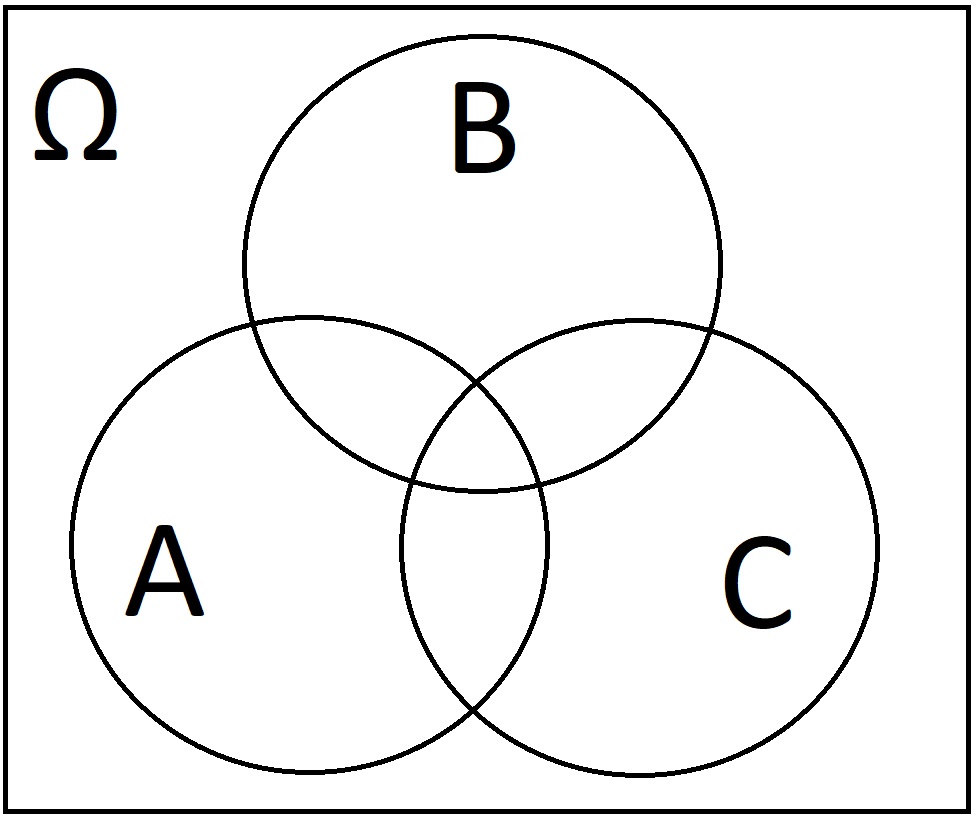
Write down the sets represented by the following Venn diagrams:

Question E

Consider \(A\) and \(B\) to be general non-empty sets, and the universal set to be \(\Omega\). State whether the following statements are true or false.

If \(A \subset B\) then \(A \cap B = \emptyset\).
It is true that \(A \cup B = B \cup A\)
It is true that \(A \cap B = B \cap A\)
\(P(A) \in A\), where \(P(A)\) is the power set of \(A\).
If \(A\) is finite and \(B\) is infinite, then \(A \cup B\) is infinite.
If \(x \in A\) and \(y \in A\), then \(x = y\).
If \(A\) and \(B\) are form a partition over \(\Omega\), then \(B = \overline{A}\).
If \(A\) and \(B\) are mutually exclusive then \(A \cup B = \emptyset\).
\(\lvert A \setminus B \rvert = \lvert B \setminus A \rvert\).
If \(A \subset B\) then \(A \cup B = B\).