Tutorial 4 - Probability Distributions
Question A
Consider the following game of wheel of fortune:
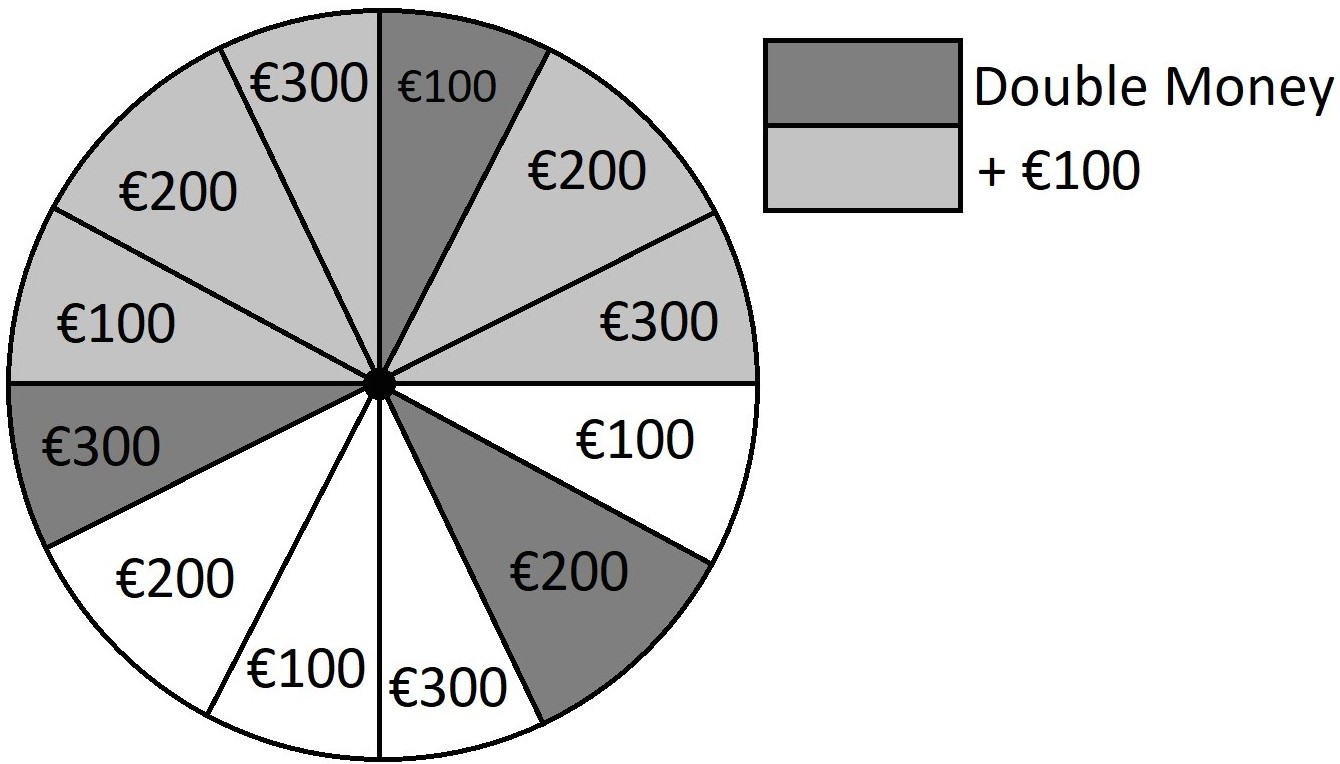
The wheel can land on each segment and they are equally likely. Players win the amount of money labelled on the segment, with the modifiers (+€100 or double money) on the corresponding coloured segments.
- Write down the pmf and cdf of the outcome.
- Calculate the expected outcome.
- Calculate the variance of the outcome.
- What’s the most amount of money the casino can charge to spin the weel so that at least 30% of all players make a profit?
- What is the mean profit?
- If each contestant played the game \(n\) times and the prizes cumulated, what would you expect the distribution of the outcome to be if \(n\) was very very large?
Question B
Let X be the random variable representing the minimum value of two dice.
- Write down the pmf of X.
- Calculate \(\mathbb{E}[X]\) and \(Var(X)\).
- Find \(\mathbb{P}(X \leq 3)\).
- If \(Y\) is the is the minimum value of \(n\) dice thrown at the same time, what would you expect the distribution of \(Y\) to be if \(n\) was very very large?
Question C
It is known that the height of an appartment building in in Manhattan follows a Normal distribution, with mean 46.3m and standard deviation 10m. A building is chosen at random.
- What is the probability that it is between 36.3m and 56.3m?
- What is the probability that it is taller than 63m?
- What is the probability that it is shorter than 20m?
- What is the probability that it is between 40m and 55m?
- What is the probability that it is taller than 70m or shorter than 10m?
- If I choose a Manhattan resident at random, would I expect the mean height of their building to be 46.3m? Explain your answer.
- Give a reason why the height of Manhattan buildings cannot truly follow a Normal distribution.
Question D
It is known that the price of artworks sold at an auction in 2019 was Normally distirbuted with mean £1300 and standard deviation £250.
- Roughly what proportion of artworks were sold for more than £1300?
- Give the first and third quartiles of the distribution.
- What proportion of artworks were sold for more than £1000?
- What proportion of artworks were sold for more than £2000?