Effaith amrywiant ar amseroedd aros
Wythnos yma mynychais i’r Ysgol Haf Ymchwil Weithrediadol Gofal Iechyd CHOIR ym Mhrifysgol Twente, yr Iseldiroedd. Roedd hwn yn gyfle gwych lle dysgon ni am dechnegau ymchwil weithrediadol a defnyddiwyd mewn ymarfer ac mewn ymchwil i ddatrys problemau gofal iechyd (roedd yna sesiynau ar efelychiad, prosesau penderfynu Markov, optimeiddio gwrthdro, a mwy). Trafodon ni sut i ymgysylltu’n well gyda gweithwyr gofal iechyd i uchafu effaith ein gwaith, ac yn fwy pwysig cwrdd â myfyrwyr PhD ac ymchwilwyr rhyfeddol eraill o bedwar ban y byd.
Arweiniodd Prof. Erwin Hans trafodaeth fywiog ar sut i wneud yr effaith fwyaf gyda’n gwaith. Amlinellodd e lwyddiannau’r grŵp CHOIR, a phwysigrwydd deall gwahanol ieithoedd a siaradwyd gan weithwyr gofal iechyd ac ymchwilwyr weithrediadol. Un agwedd bwysig o hwn yw bod gweithwyr gofal iechyd yn hoffi siarad am “optimeiddio” rhywbeth, tra bod ymchwilwyr weithrediadol yn tueddu meddwl am “lleihau amrywiant”, a bod hwn yn tueddu cael mwy o effaith ar systemau. Mae hwn yn amlwg mewn systemau ciwio, ac mae’r cofnod hwn yn trio dangos hwn.
Ciwiau penderfynol vs. Markovaidd
Dyma enghraifft rydw i’n hoffi rhoi i esbonio i ffrindiau beth rydw i’n astudio: Ystyriwch giw gydag un gweinydd. Mae cwsmeriaid yn cyrraedd pob 10 munud, ac mae gwasanaeth yn para 10 munud. Ni ddisgwylir ciw i ffurfio, gan fod cwsmeriaid yn dilyn patrwm “un mewn - un mas”.
Mae hwn ond yn wir yn yr achos penderfynol, lle mae cwsmeriaid yn cyrraedd yn union 10 munud ar wahân, ac mae cwsmeriaid yn gwario 10 munud yn union yn derbyn gwasanaeth.
Nawr gadewch i ni ystyried y model mathemategol symlaf o giw ar hap. Mae yna un gweinydd. Mae cwsmeriaid yn cyrraedd ar hap, tua 10 munud ar wahân ar gyfartaledd. Mae cwsmeriaid yn treulio rhyw cyfnod amser ar hap yn derbyn gwasanaeth, sy’n para 10 munud ar gyfartaledd. Fan hyn, pan rwy’n dweud “ar hap”, rwy’n golygu fod y dosraniad yn dilyn dosraniad esbonyddol. Mae mathemategwyr yn galw hwn yn system \(M/M/1\), (dyfodiadau a gwasanaethau Markovaidd) ac maent wedi deillio mynegiadau ar gyfer amser aros disgwyliedig y system:
\[\mathbb{E}\left[W_q\right] = \frac{\rho}{\mu\left(1-\rho\right)}\] \[\rho = \frac{\lambda}{\mu}\]Lle \(\lambda\) yw’r gyfradd dyfodi a \(\mu\) yw’r gyfradd gweini. Yn ein system ni \(\lambda = 0.1\) (cwsmer yn cyrraedd pob 10 munud) a \(\mu = 0.1\) (mae gwasanaeth yn para 10 munud). Yn gyflym gwelwn fod y dwysedd traffig \(\rho = 1\), ac mae’r mynegiad ar gyfer yr amser aros disgwyliedig \(\mathbb{E}\left[W_q\right]\) yn agosâi at anfeidredd.
Mae ychwanegu amrywiant i’r system yma yn achosi i gwsmeriaid aros am faint anfeidraidd o amser!
Effaith cyffredinol amrywiant
Byddaf nawr yn defnyddio Python a’r llyfrgell efelychu ciwiau Ciw i dangos sut all lleihau amrywiant mewn system bod yn ddigonol i leihau amseroedd aros. Dyma cofnod blog tebyg ar y pwnc gan Vincent Knight. Eto, ystyriwch giw gydag un gweinydd.
Amnewidiaf y dosraniad amser gwasanaeth gyda dosraniad Gama, er mwyn gallu cynyddu amrywiant yr amseroedd aros heb gynyddu’r amser gwasanaeth cymedrig. Mae dosraniadau Gama yn cymryd dau baramedr \(\alpha\) a \(\beta\), a rhoddir ei chymedr ac amrywiant gan y mynegiadau isod:
\[\mu = \alpha \beta\] \[\sigma^2 = \alpha \beta^2\]Gellir aildrefnu i roi:
\[\alpha = \frac{\mu^2}{\sigma^2}\] \[\beta = \frac{\sigma^2}{\mu}\]Gan ddewis cyfradd dyfodi o 0.25, a chyfradd gwasanaeth o 2, efelychaf y system yn cynyddu’r amrywiant, am 100 uned amser. Noder defnyddiaf arbrofion, amser cynhesu ac oeri i ddilyn arferion efelychu gorau. Mae’r cod isod:
>>> import ciw
>>> import numpy as np
>>> assert ciw.__version__ == '1.1.2'
>>> means = [1 for _ in range(1, 21)]
>>> variances = [0.25 * i for i in range(1, 21)]
>>> average_waits = []
>>> for v, m in zip(variances, means):
... a = (m ** 2) / v
... b = v / m
... N = ciw.create_network(
... Arrival_distributions=[['Exponential', 0.25]],
... Service_distributions=[['Gamma', a, b]],
... Number_of_servers=[1]
... )
... average_waits.append([])
... for trial in range(50):
... ciw.seed(trial)
... Q = ciw.Simulation(N)
... Q.simulate_until_max_time(140)
... recs = Q.get_all_records()
... waits = [r.waiting_time for r in recs if r.arrival_date > 20 if r.arrival_date < 120]
... average_waits[-1].append(np.mean(waits))Gan ddefnyddio seaborn gallaf plotio’r amseroedd
aros cymedrig ar gyfer pob gwerth \(\sigma^2\).
Mae ffwythiant tsplot Seaborn hefyd yn rhoi’r cyfyngau hyder 95%.
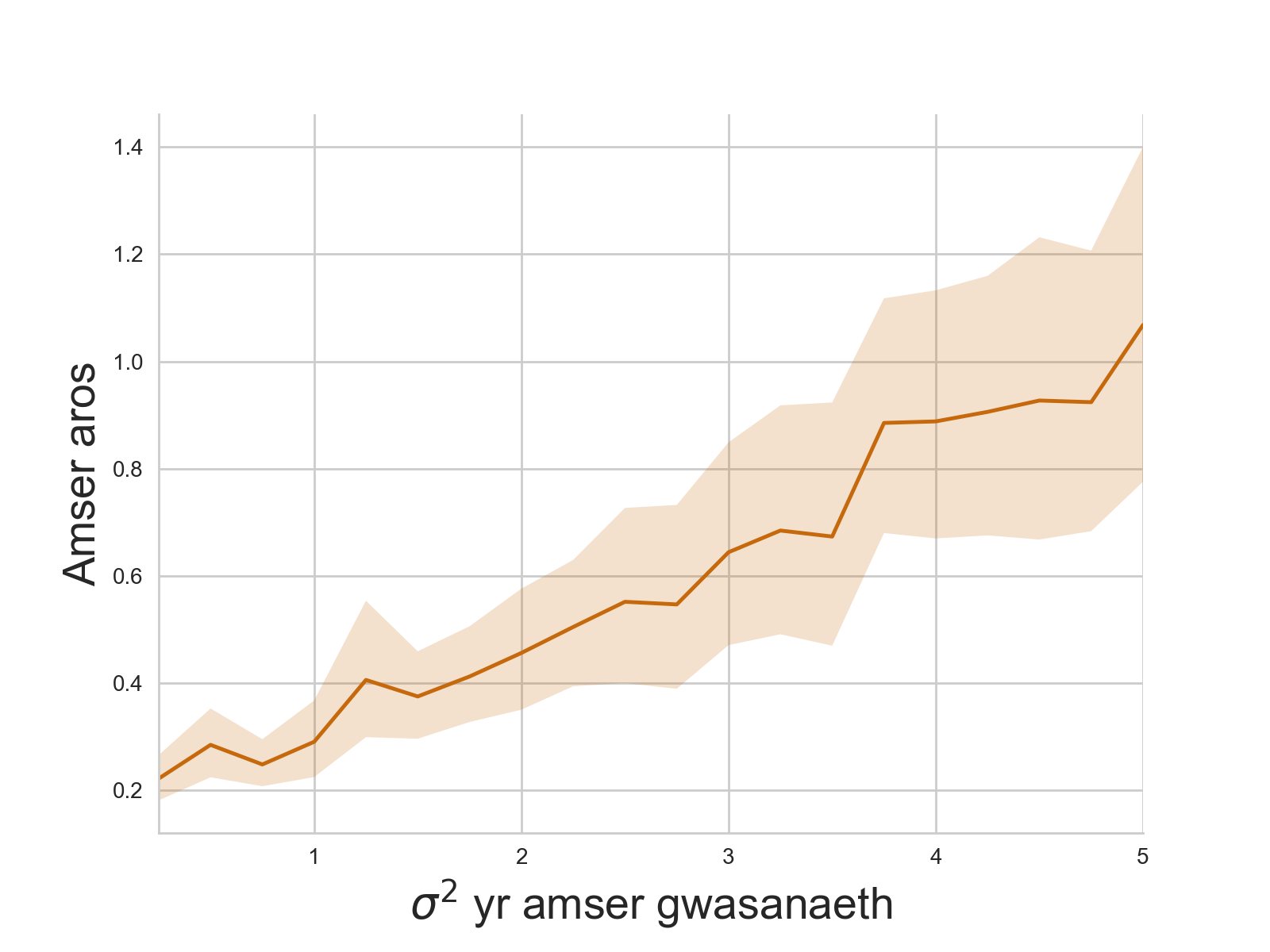
Mae cynyddu’r amrywiant, wrth gadw’r cymedr yn sefydlog, yn cynyddu’r amser aros. Gyda’r paramedrau a dewiswyd, mae cynyddu’r amrywiant gan ffactor o bump yn achosi’r amser aros cynyddu gan ffactor o bedwar. (Nodwch fod defnyddio’r dosraniad Gama yn y ffordd yma hefyd yn newid priodweddau arall o’r dosraniad, er enghraifft ei sgiwedd a chwrtosis). Mae’r cynnydd yn amrywiant yma hefyd yn cynyddu amrywiant yr amseroedd aros.
Mae arbrawf arall yn dangos effeithiau tebyg wrth gynyddu’r amrywiant yn y dyfodiadau:
>>> means = [2 for _ in range(1, 21)]
>>> variances = [0.25*i for i in range(1, 21)]
>>> average_waits = []
>>> for v, m in zip(variances, means):
... a = (m ** 2) / v
... b = v / m
... N = ciw.create_network(
... Arrival_distributions=[['Gamma', a, b]],
... Service_distributions=[['Exponential', 2]],
... Number_of_servers=[1]
... )
... average_waits.append([])
... for trial in range(50):
... ciw.seed(trial)
... Q = ciw.Simulation(N)
... Q.simulate_until_max_time(140)
... recs = Q.get_all_records()
... waits = [r.waiting_time for r in recs if r.arrival_date > 20 if r.arrival_date < 120]
... average_waits[-1].append(np.mean(waits))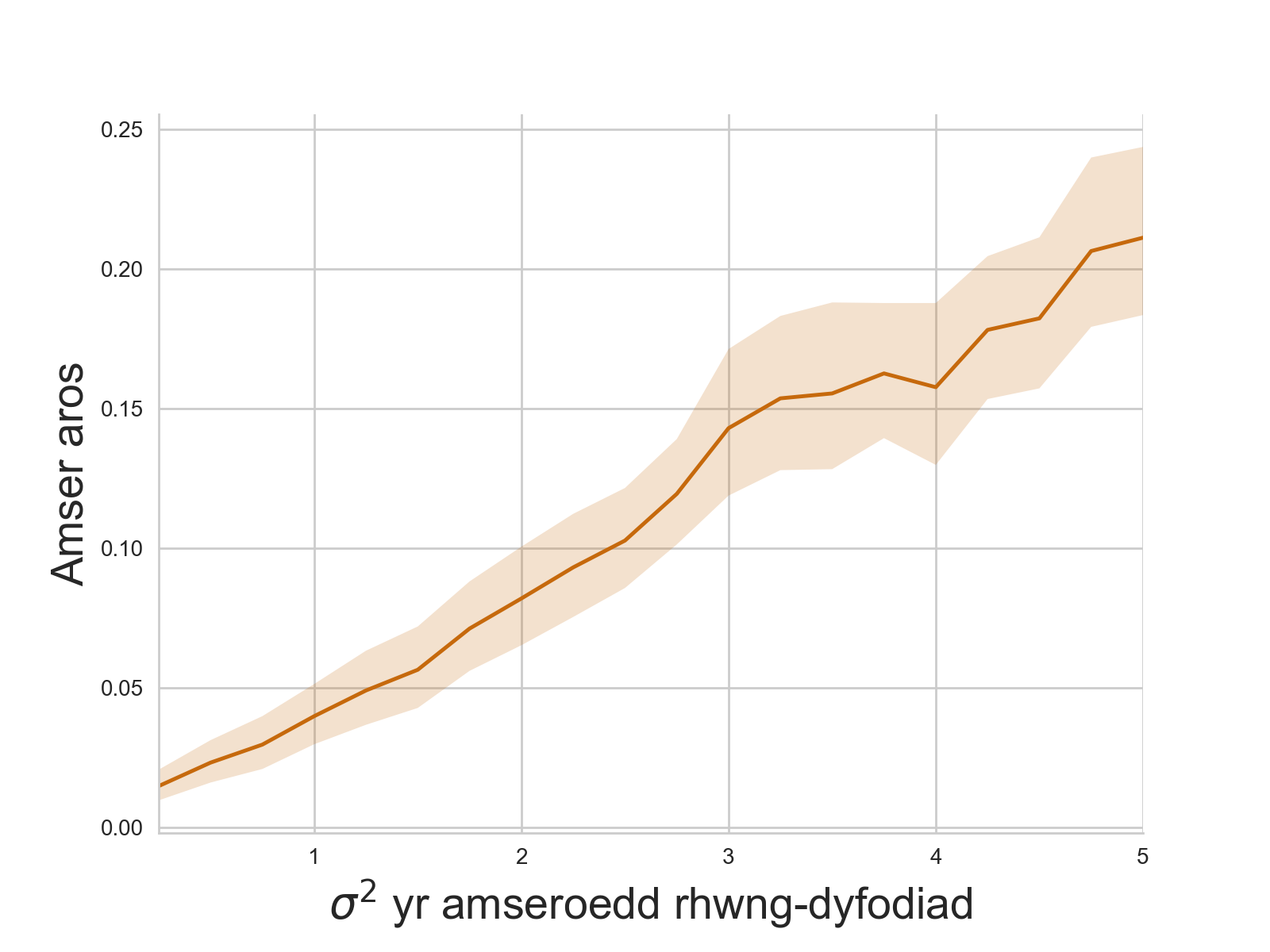
Eto, mae cynyddu’r amrywiant yn cynyddu’r amseroedd aros.
Mae’r effeithiau yma yn amlwg mewn fformiwla Kingman, sy’n rhoi amcangyfrif amser aros ciw \(G/G/1\) (dosraniadau cyffredinol ar gyfer dyfodiadau a gwasanaethau):
\[\mathbb{E}\left[W_q^{G/G/1}\right] \approx \mathbb{E}\left[W_q^{M/M/1}\right] \left(\frac{c_a^2 + c_s^2}{2}\right)\]lle \(c_a^2\) yw cyfernod amrywiant yr amseroedd rhwng-dyfodiad, a \(c_s^2\) yw cyfernod amrywiant yr amseroedd gwasanaeth. Hynny yw’r amrywiant wedi rhannu gyda’r cymedr wedi sgwario. Felly wrth i amrywiant y dyfodiadau a’r gwasanaethau cynyddu, mae’r cyfernodau amrywiant cyfatebol hefyd yn cynyddu, ac felly’r amser aros cymedrig.
Mae’r systemau enghreifftiol yma yn fach, ond defnyddir i dangos pwysigrwydd ystyried amrywiant, yn enwedig mewn systemau gofal iechyd cymhleth lle mae amrywioldeb yn codi’n aml: cleifion argyfwng, salwch yn y gweithlu, cleifion ddim yn ymddangos am lawdriniaeth, ayyb. Mae hwn yn uwcholeuo peryglon dibynnu ar gyfartaleddau yn unig.