Schelling's segregation model
Over the last few weeks I have had a number of conversations about agent based modelling (ABM). This is a topic that seems interesting, and though I have not used it in my research, is something that I am keen to use in the future.
In order to increase my understanding of ABM, I decided to reproduce an early, and now famous agent based model: Schelling’s Segregation Model. Thomas Schelling was an economist who first devised the model, which was used to show that a small preference for a neighbour to be of the same class/race as yourself can lead to total segregation. Schelling played out the model using coins on graph paper, however there have been numerous computer simulation models run since.
The model is defined:
- A grid of squares represents the world, with each square representing a plot of land in which an agent can live.
- The world is populated (randomly initially) with a number of different kinds of agents (in our case 2), leaving a proportion of the squares vacant.
- The agents have a certain preference for the number of their immediate neighbours (agents living in the plots of land directly adjacent, including diagonally) to be of the same kind as themselves. If the number of similar neighbours is below this preference, then that agent becomes unhappy.
- Each turn, all* unhappy agents move to a randomly selected vacant plot.
I implemented this in Python, using objects as agents.
For ease of coding my model assumes the world is a torus, that is the extreme
left are neighbours to the extreme right, and the extreme top are neighbours
with the extreme bottom.
I also bend the rules slightly, and instead of all unhappy agents moving each
turn, only some agents move, depending on whether the number of unhappy agents
exceeds the number of vacant plots.
The code defining the Agent and the World classes in which the agents live
are given at the end of this post.
Object-orientated programming is an intuitive way of implementing ABM as objects themselves become the agents: object attributes are the properties of the agents, and object methods are the things the agents do.
Lets see the simulation in action. White squares represent vacant plots, yellow and purple squares represent the plots where the two different kinds of agents live. This animation shows a world grid of 80x80 squares, where agents have a preference for 70% similar neighbours:

The simulation is stopped once 99.995% of agents are happy. The resulting population has a mean neighbour similarity, or mean happiness of 99.51%, much larger than the 70% preference.
Experiments can be run to show how the model behaves with different preferences. These experiments were run on world grid of 40x40 squares:
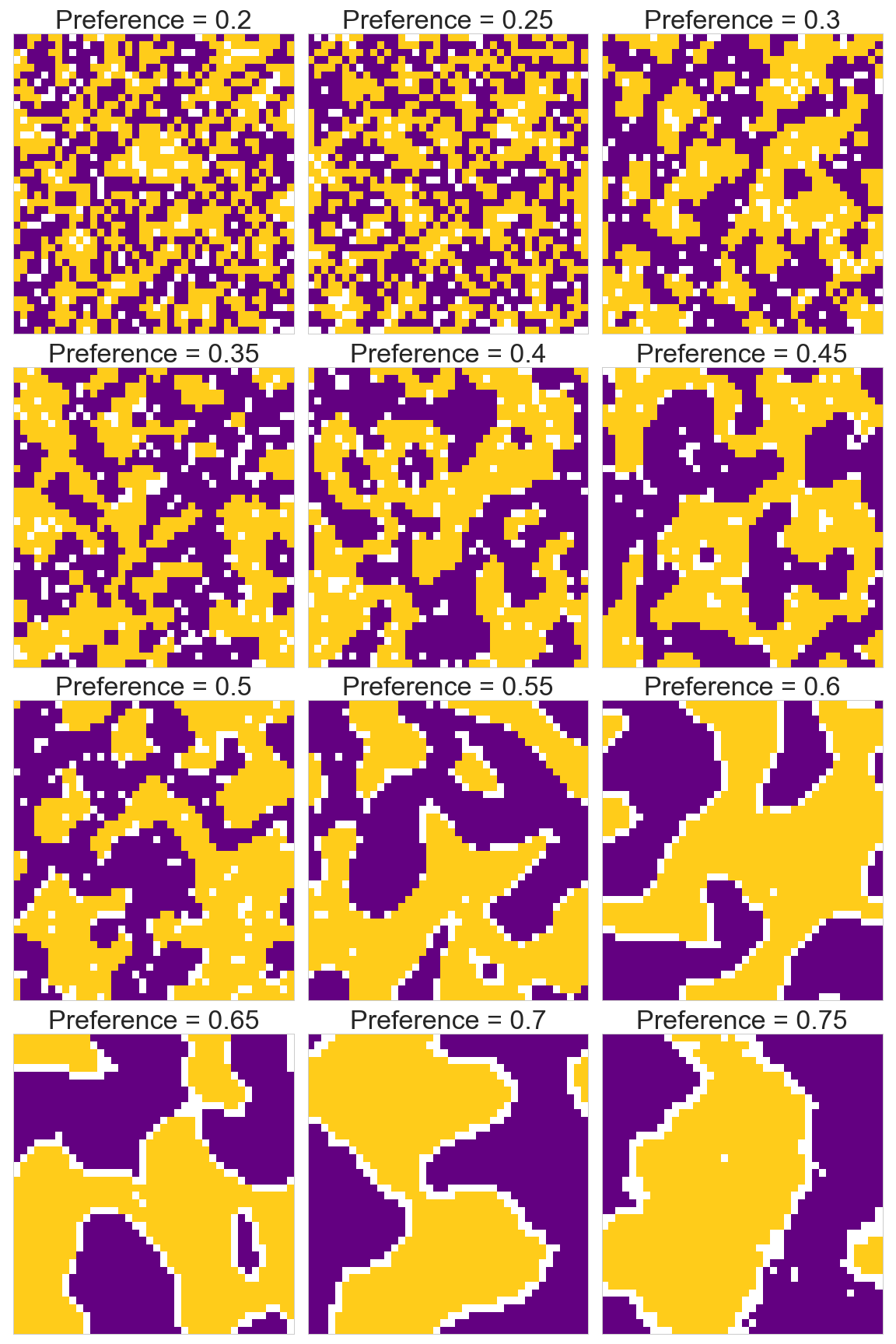
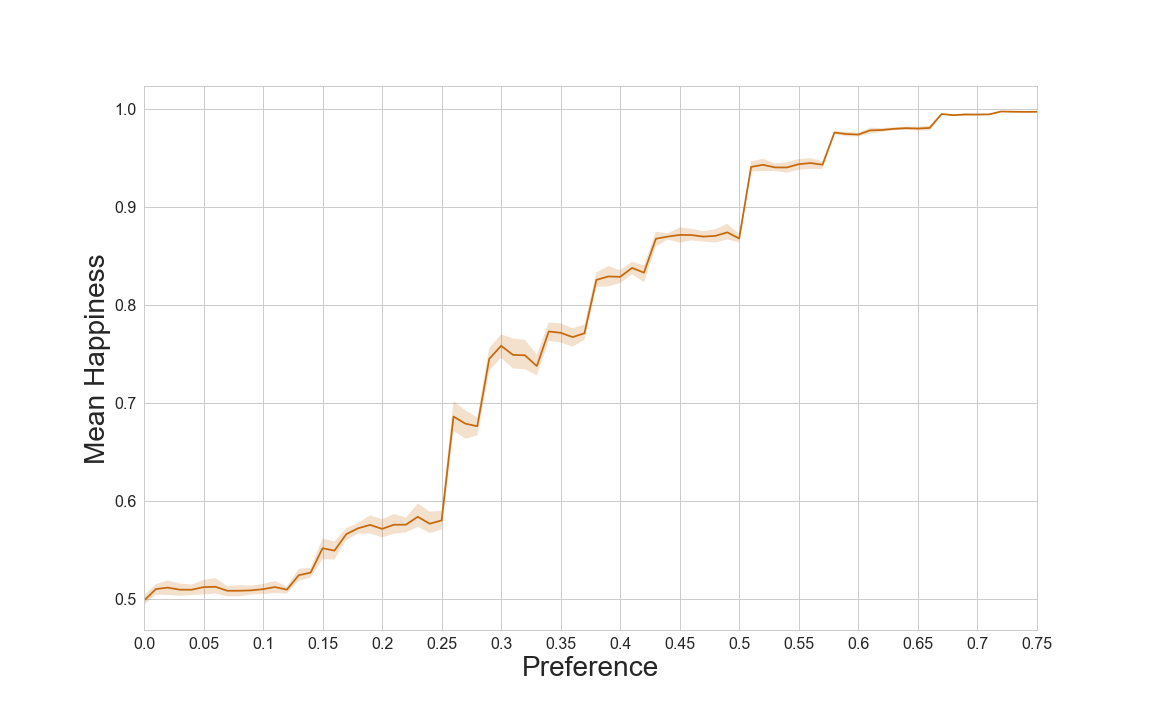
As the individual agents’ preferences are increased, the world becomes more and more segregated. We can see in the plot below that as agents’ preference is increased, the resulting world’s mean happiness also increases. The world’s mean happiness always remains well above the individual agents’ preference:
Another measure of segregation is the number of ‘colonies’ formed. That is how many clusters of similar agents are formed. For the purpose of illustration, I will very loosely define a colony as follows:
Imagine the grid of squares as a network of vertices, where there is an edge between two vertices if those squares are neighbours and they are occupied by agents of the same kind. Then a colony is a connected component of that network.
Using NetworkX getting the number of connected components is simple. The plot below shows that the number of colonies dramatically decrease as agents’ preference increases, and that the largest decrease actually occurs at a very low preference level:
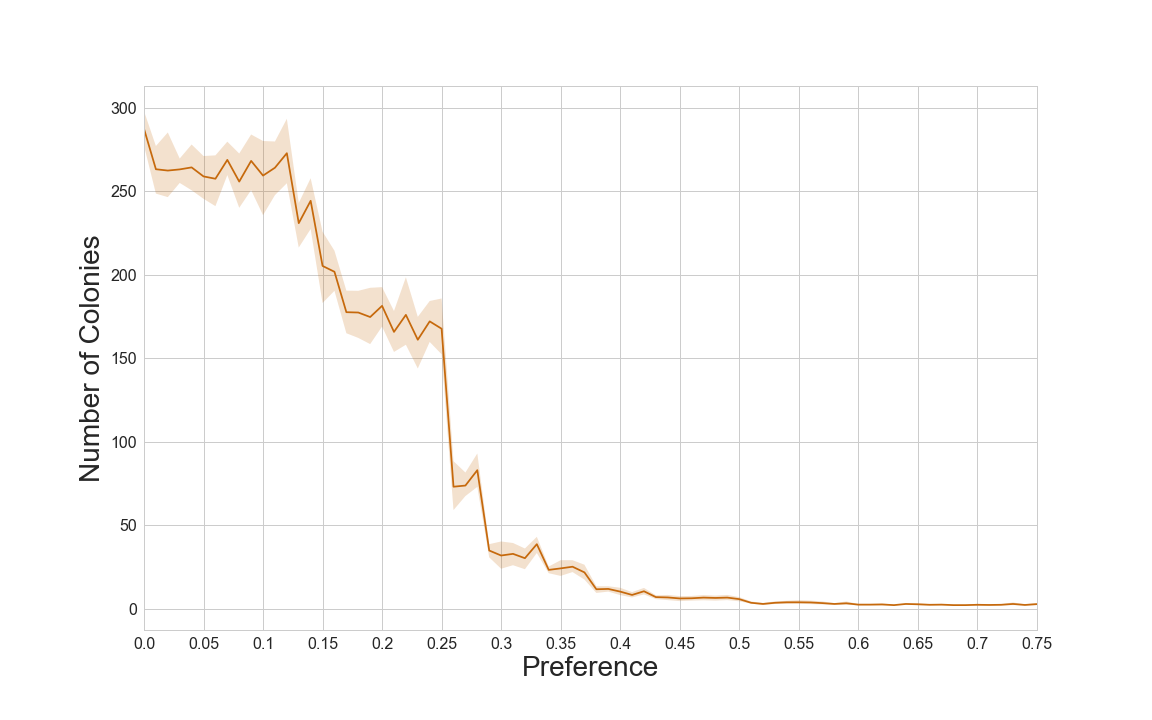
Loosely, a world populated by agents with 30% preference for similar neighbours results in a world 40 times more segregated than a world populated by agents with 10% preference for similar neighbours.
This ABM shows emergent behaviour. No one told the agents to segregate themselves and form colonies. The agents were given simple rules: look at neighbours and decide if happy, if unhappy move. System wide behaviour, segregation and colony formation, emerged from these simple rules. This is like how societal behaviour emerges from individual actions.
Here is an interesting list of NetLogo agent based models. You will see how these types of models have been used fields as far apart as biology, social sciences, and mathematics. They are being used in operational research too, which is something I hope to read more about.
All the code used to produce the results of this post is available on Github here.
Code defining Agent and World classes:
class Agent:
def __init__(self, x, y, kind, preference, world):
self.x = x
self.y = y
self.kind = kind
self.preference = preference
self.world = world
def know_neighbours(self):
self.neighbours = [self.world.coords[x % self.world.size, y % self.world.size]
for x, y in itertools.product(range(self.x-1, self.x+2),
range(self.y-1, self.y+2))]
def swap(self, partner):
self.kind, partner.kind = partner.kind, self.kind
def happiness(self):
neighbour_kinds = [n.kind for n in self.neighbours]
numsame = neighbour_kinds.count(self.kind)
numvacant = neighbour_kinds.count(0)
if numvacant == 8:
if self.vacant():
return 1.0
return 0.0
return (numsame - 1) / (8 - numvacant)
def dissatisfied(self):
return self.happiness() < self.preference
def vacant(self):
return self.kind == 0class World:
def __init__(self, size, kinds, probs, preference):
self.size = size
self.preference = preference
self.coords = self.populate_world(kinds, probs, preference)
[a.know_neighbours() for row in self.coords for a in row]
self.num_dissatisfied = size ** 2
self.num_vacant = sum([a.vacant() for row in self.coords for a in row])
def populate_world(self, kinds, probs, preference):
return np.array([[Agent(x, y, np.random.choice(kinds, p=probs), preference, self)
for y in range(self.size)] for x in range(self.size)])
def atlas(self):
return np.array([[a.kind for a in row] for row in self.coords])
def happiness_distribution(self):
return [a.happiness() for row in self.coords for a in row if not a.vacant()]
def advance_turn(self):
dissatisfied = []
vacant = []
for row in self.coords:
for a in row:
if a.vacant():
vacant.append(a)
elif a.dissatisfied():
dissatisfied.append(a)
self.num_dissatisfied = len(dissatisfied)
np.random.shuffle(dissatisfied)
np.random.shuffle(vacant)
num_swap = min(self.num_dissatisfied, self.num_vacant)
for indx in range(num_swap):
dissatisfied[indx].swap(vacant[indx])
def play(self, threshold=0.01):
while self.num_dissatisfied / (self.size ** 2) > threshold:
self.advance_turn()