When should I take out life insurance?
When is the best age to begin a life insurance policy? If I begin the policy too young I’ll end up paying in a lot more, with little risk of dying young. However if I plan to begin the policy at a later age then there is a higher risk of me dying before I take out the policy, leaving my descendants with nothing. Using some probability I’ll find a naïve optimal age to begin a life insurance policy.
Let’s assume I’m planning on taking out a whole life level policy; so I’ll pay a fixed amount every month of my life until I die; and my descendants will receive a fixed lump sum once I pass. Using dubious sources the average monthly cost is £30.40, for a policy worth £100,000. (There are a huge amount of policies out there, some much cheaper! This is used as an illustrative example).
>>> year_cost = 30.40 * 12
>>> payoff_after_death = 100000In this post we’ll be taking the product of a list of numbers, so define a function to do just that:
from math import log, exp
def prod(data):
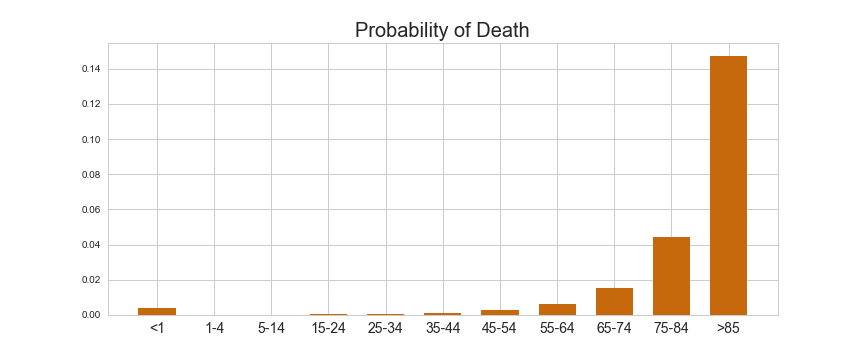
return exp(sum(map(log, data)))First let’s define \(m_i\) as the probability of dying at age \(i\).
Using ONS data this is freely available, as described in a
previous blog post (stored as the list mortalities
in this code).
Say I plan to take out an insurance policy at age \(i\), define \(s_i\) as my probability of surviving up to the point I take out the policy:
\[s_i = \prod_{j=0}^i \left(1 - m_i\right)\]>>> prob_survive_to_insurance = [prod([1 - m for m in mortalities[:age_start]]) for age_start in range(102)]Similarly, if I live to take the policy out at age \(i\), my chance of living until age \(j\) is \(\prod_{k=i}^j \left(1 - m_{i + k}\right)\). And so my expected number of years left to live after taking out my policy at age \(i\) is:
\[y_i = \sum_{j = i}^\infty \prod_{k=i}^j \left(1 - m_{i + k}\right)\]>>> expected_years_left_after_policy_start = [sum([prod([1 - m for m in mortalities[age_start:age_die]]) for age_die in range(age_start, 102)]) for age_start in range(102)]Let’s say my policy costs \(\kappa\) pounds a month, and once I’m dead my descendants will receive a lump sum of \(F\) pounds.
After beginning a policy at age \(i\) my expected lifetime contribution is:
\[c_i = \kappa y_i\]>>> expected_lifetime_payment = [year_cost * years for years in expected_years_left_after_policy_start]And so my descendants’ expected profit, \(p_i\), is \(F - c_i\) if I live to the age \(i\) where I begin my policy, and £0 is I don’t:
\[p_i = s_i \left(F - c_i\right)\]>>> expected_payoff_per_year = [s * (payoff_after_death - cost) for s, cost in zip(prob_survive_to_insurance, expected_lifetime_payment)]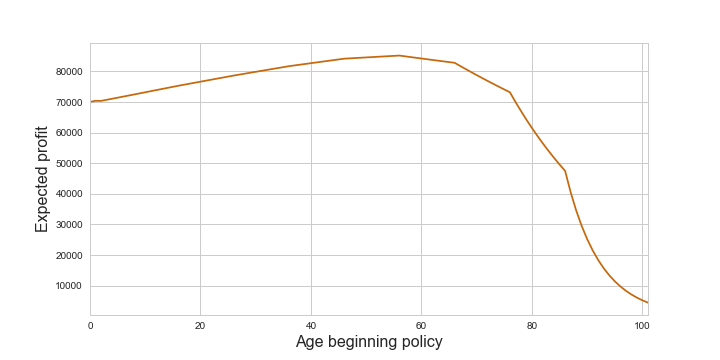
From this function we can find the age at which to begin the policy in order to maximise expected profit:
>>> max_payoff = max(expected_payoff_per_year)
>>> optimal_age = expected_payoff_per_year.index(max_payoff)Which gives the optimal age to begin this policy at 56, yielding a profit of £85,191.49.
Note: This post is a huge simplification of real life, ignoring many important things such as interest rates. It also assumes that I don’t have any debts, morgages etc. This post should not be taken as financial advice!