Pryd dylaf i gymryd mas yswiriant bywyd?
Beth yw’r oedran gorau i ddechrau polisi yswiriant bywyd? Os dechreuaf i’r polisi yn rhy ifanc byddaf yn dod i ben yn talu lot mwy, gyda risg bach iawn o farw’n ifanc. Ond os cynlluniaf i ddechrau’r polisi yn rhy hen, mae mwy o risg o farw cyn dechrau’r polisi, gan adael fy nheulu gyda dim. Gan ddefnyddio tebygolrwydd byddaf yn ffeindio oedran gorau naïf o bryd i ddechrau polisi yswiriant bywyd.
Tybiwch fy mod am ddechrau polisi lefel holl fywyd; felly talaf swm sefydlog pob mis o’m mywyd nes i mi farw; a bydd fy nheulu yn derbyn cyfandaliad sefydlog unwaith i mi farw. Gan ddefnyddio ffynonellau amheus y gost fisol gymedrig yw £30.40, ar gyfer polisi werth £100,000. (Mae nifer helaeth o bolisïau ar gael, rhai llawer rhatach! Defnyddiwn hwn fel enghraifft yn unig).
>>> year_cost = 30.40 * 12
>>> payoff_after_death = 100000Yn y post yma byddwn yn cymryd lluoswm rhestr o rifau, felly diffiniwn ffwythiant i wneud hynny:
from math import log, exp
def prod(data):
return exp(sum(map(log, data)))Yn gyntaf diffiniwn \(m_i\) fel y tebygolrwydd o farw oedran \(i\).
Yn defnyddio data ONS mae hwn ar gael am ddim, fel y disgrifir mewn
cofnod blog blaenorol (wedi’i storio fel y
rhestr mortalities yn y cod yma).
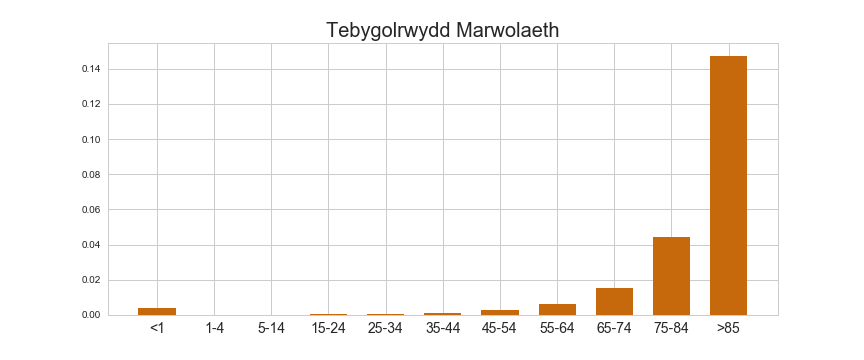
Os cynlluniaf ddechrau polisi yswiriant oedran \(i\), diffiniwn \(s_i\) fel y tebygolrwydd o oroesi nes i mi ddechrau’r polisi:
\[s_i = \prod_{j=0}^i \left(1 - m_i\right)\]>>> prob_survive_to_insurance = [prod([1 - m for m in mortalities[:age_start]]) for age_start in range(102)]Yn debyg, os dechreuaf y polisi oedran \(i\), y siawns o fyw nes oedran \(j\) yw \(\prod_{k=i}^j \left(1 - m_{i + k}\right)\). Ac felly’r nifer o flynyddoedd disgwyliedig i fyw ar ôl dechrau fy mholisi oedran \(i\) yw:
\[y_i = \sum_{j = i}^\infty \prod_{k=i}^j \left(1 - m_{i + k}\right)\]>>> expected_years_left_after_policy_start = [sum([prod([1 - m for m in mortalities[age_start:age_die]]) for age_die in range(age_start, 102)]) for age_start in range(102)]Tybiwch fod y polisi yn costio \(\kappa\) punt y mis, ac unwaith rydw i wedi marw bydd fy nheulu yn derbyn cyfandaliad \(F\) punt.
Ar ôl dechrau’r polisi oedran \(i\) fy nghyfraniad disgwyliedig oes yw:
\[c_i = \kappa y_i\]>>> expected_lifetime_payment = [year_cost * years for years in expected_years_left_after_policy_start]Ac felly elw disgwyliedig fy nheulu, \(p_i\), yw \(F - c_i\) os byddaf yn byw nes oedran \(i\) lle dechreuaf y polisi, a £0 fel arall:
\[p_i = s_i \left(F - c_i\right)\]>>> expected_payoff_per_year = [s * (payoff_after_death - cost) for s, cost in zip(prob_survive_to_insurance, expected_lifetime_payment)]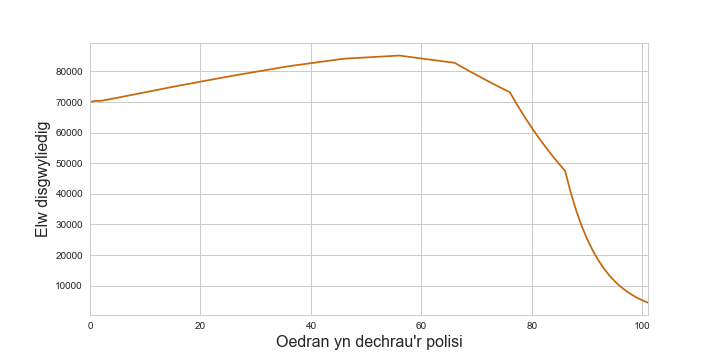
O’r ffwythiant yma gallwn ffeindio’r oedran gorau i ddechrau’r polisi er mwyn macsimeiddio’r elw disgwyliedig:
>>> max_payoff = max(expected_payoff_per_year)
>>> optimal_age = expected_payoff_per_year.index(max_payoff)Sy’n rhoi oedran gorau i ddechrau polisi o 56, yn rhoi elw disgwyliedig o £85,191.49.
Noder: Mae’r blog yma wedi symleiddio bywyd go iawn yn fawr iawn, gan anwybyddu nifer o bethau pwysig megis cyfraddau llog. Mae hefyd yn tybio does gen i ddim dyledion, morgeisi, ayyb. Peidiwch gymryd y cofnod blog yma fel cyngor ariannol!